Python 中的单神经元神经网络

神经网络是深度学习非常重要的核心；它在许多不同领域都有许多实际应用。如今，这些网络被用于图像分类、语音识别、目标检测等。

让我们来了解一下它是什么以及它是如何工作的？

这个网络有不同的组件。它们如下所示 -

  • 输入层，x
  • 任意数量的隐藏层
  • 输出层，ŷ
  • 每层之间的一组权重和偏差，由 W 和 b 定义
  • 接下来是为每个隐藏层选择激活函数，σ。

在此图中，展示了 2 层神经网络（在计算神经网络中的层数时，通常不包括输入层）

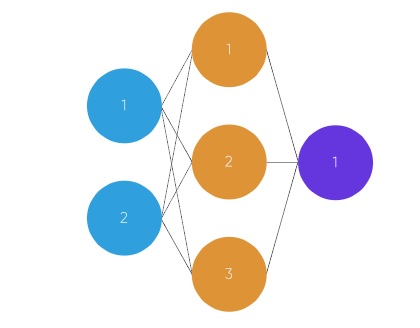
Neuron Neural Network

在此图中，圆圈代表神经元，线条代表突触。突触用于将输入和权重相乘。我们将权重视为神经元之间连接的“强度”。权重定义了神经网络的输出。

以下是简单的前馈神经网络工作原理的简要概述 -

当我们使用前馈神经网络时，我们必须遵循一些步骤。

  • 首先将输入作为矩阵（数字的二维数组）

  • 接下来是将输入乘以一组权重。

  • 接下来应用激活函数。

  • 返回输出。

  • 接下来计算误差，它是数据期望输出与预测输出之间的差值。

  • 并且权重会根据误差稍作调整。

  • 为了训练，这个过程会重复 1,000+ 次，并且训练的数据越多，我们的输出就会越准确。

学习时间，睡眠时间（输入）测试分数（输出）

2, 992
1, 586
3, 689
4, 8?

示例代码

from numpy import exp, array, random, dot, tanh
class my_network():
   def __init__(self):
      random.seed(1)
      # 3x1 Weight matrix
      self.weight_matrix = 2 * random.random((3, 1)) - 1
      defmy_tanh(self, x):
      return tanh(x)
      defmy_tanh_derivative(self, x):
   return 1.0 - tanh(x) ** 2
      # forward propagation
      defmy_forward_propagation(self, inputs):
   return self.my_tanh(dot(inputs, self.weight_matrix))
      # training the neural network.
      deftrain(self, train_inputs, train_outputs,
      num_train_iterations):
   for iteration in range(num_train_iterations):
      output = self.my_forward_propagation(train_inputs)
      # Calculate the error in the output.
      error = train_outputs - output
      adjustment = dot(train_inputs.T, error *self.my_tanh_derivative(output))
      # Adjust the weight matrix
      self.weight_matrix += adjustment
      # Driver Code
   if __name__ == "__main__":
      my_neural = my_network()
      print ('Random weights when training has started')
   print (my_neural.weight_matrix)
      train_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
      train_outputs = array([[0, 1, 1, 0]]).T
      my_neural.train(train_inputs, train_outputs, 10000)
   print ('Displaying new weights after training')
      print (my_neural.weight_matrix)
         # Test the neural network with a new situation.
         print ("Testing network on new examples ->")
print (my_neural.my_forward_propagation(array([1, 0, 0])))

输出

Random weights when training has started
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
Displaying new weights after training
[[5.39428067]
[0.19482422]
[0.34317086]]
Testing network on new examples ->
[0.99995873]

更新于: 2020年6月26日

675 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习
广告