算术几何数列

---

简介

算术几何级数是一个数列，其中每个元素的排列顺序使得相邻两项的比值始终保持不变。

在数学中，数列是有序排列的一组数，数列中每个元素都对应着下一个元素的位置和值。数列是高等数学中计算无穷级数的基础。在本教程中，我们将学习算术级数、第n项公式、算术级数n项之和以及一些已解决的例子。

数列

可以按一定顺序排列的一组数，数列中的元素可以以任何方式重复。数列本身没有值，而是每个元素都由一个公式定义，并可以根据该公式计算。级数可以分为三种类型：算术级数、几何级数和调和级数。

算术数列 (AP)

也称为“算术级数”，它是一个数列，其中每个元素的排列顺序使得该数列中每一项与前一项的差值相同。级数中的每个元素都称为“项”。

例如：2, 5, 8, 11, 14, 17, 20……

上述数列中每一项与其前一项或后一项的差值为3，这在算术级数中称为“公差”。公差是算术数列中相邻两数的差值。我们也可以说，数列中的任何元素都可以通过从其相邻元素中加或减一个特定数字来计算。

假设有一个数列：

x₁,x₂,x₃,x₄,x₅,...........x_n，其中x₁是第一项，x_n是最后一项。

设“a”为上述数列中的公差。

那么：

$$\mathrm{x_2= x_1+a,}$$

$$\mathrm{x_3=x_2+a,}$$

$$\mathrm{x_4=x_3+a,}$$

$$\mathrm{\vdots}$$

$$\mathrm{x_n=x_{n-1}+a}$$

我们也可以将数列写成：

算术级数的一般形式可以写成

$$\mathrm{x_1,x_1+a,x_1+2a,x_1+3a,x_1+4a⋯,x_1+(n-1)a.}$$

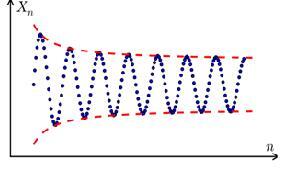
图：有限数列的值用蓝色绘制在图上。

几何数列 (GP)

一个数列，其中每个元素的排列顺序使得该数列中每一项都可以通过将其前一项或后一项乘以或除以一个特定数字来计算。

例如：3, 9, 27, 81, 243, 729……

上述数列中每一项都是其前一项的倍数，这称为数列的“公比”；在本例中为3。

让我们考虑一个数列：

x₁,x₂,x₃,x₄,x₅,...........x_n，其中x₁是第一项，x_n是最后一项。

设“m”为上述数列中的公比。

那么，我们也可以将数列写成：

$$\mathrm{x_1,x_1 m,x_1 m^2,x_1 m^3,x_1 m^4\dotso,x_1 m^{n-1}.}$$

几何级数的第n项公式

几何级数的第n项由下式给出

$$\mathrm{x_n=x_1 r^{n-1}}$$

几何级数的和，其首项为x_1，公比为r，由下式给出

$$\mathrm{S_n=\frac{x_1 (1-r^n)}{1-r}, where\: r≠1}$$

已解决的例子

1) 识别以下数列并找出数列的第n项。

• 4,15,26,41,.......

• 4, 12, 36, 108……

答案

a. 为了识别数列，我们首先应该找到相邻项之间的关系。

$$\mathrm{15-4=11}$$

$$\mathrm{26-15=11}$$

$$\mathrm{41-26=11}$$

每个相邻项之间的差值为11。因此，该数列是算术级数。

查找算术级数第n项的公式为

$$\mathrm{第n项=x_1+(n-1)a}$$

$$\mathrm{x_1=4}$$

$$\mathrm{a=11}$$

那么数列的第n项

$$\mathrm{=4+(n-1)11}$$

$$\mathrm{=11n-7}$$

因此，该数列的第n项为11n-7。

b. 为了识别数列，我们可以将除第一项外的每个元素除以前面的元素

$$\mathrm{12/4=3}$$

$$\mathrm{36/12=3}$$

$$\mathrm{108/36=3}$$

我们可以说，上述数列是公比为3的几何级数。我们知道几何级数的第n项可以由下式给出

$$\mathrm{\mathrm{x_n=x_1 r^{n-1}}}$$

将值代入方程，我们得到

$$\mathrm{x_n=4×3^{n-1}}$$

$$\mathrm{x_n=4×3^n×3^{-1}}$$

$$\mathrm{x_n=4×3^n×\frac{1}{3}}$$

$$\mathrm{x_n=\frac{4}{3}×3^n}$$

因此，给定数列的第n项 $\mathrm{x_n=\frac{4}{3}×3^n}$

2) 找出以下级数的项数。

• 1, 5, 9, 13, 17, ……….125

• 1, 2, 4, 8, 16, …………1024

答案

a. 要找出上述数列的项数，我们首先需要确定级数的类型

$$\mathrm{5-1=4}$$

$$\mathrm{9-5=4}$$

$$\mathrm{13-9=4}$$

每个相邻项之间的差值为4。因此，该数列是算术级数。

查找算术级数第n项的公式为

$$\mathrm{第n项= x_1+(n-1)a}$$

$$\mathrm{ x_1=1}$$

$$\mathrm{a=4}$$

那么数列的第n项

$$\mathrm{125=1+(n-1)4}$$

$$\mathrm{125 =4n-3}$$

$$\mathrm{4n=128}$$

$$\mathrm{n=32}$$

给定数列中有32项。

b. 为了识别数列，我们可以将除第一项外的每个元素除以前面的元素

$$\mathrm{2/1=2}$$

$$\mathrm{4/2=2}$$

$$\mathrm{8/4=2}$$

我们可以说，上述数列是公比为3的几何级数。我们知道几何级数的第n项可以由下式给出

$$\mathrm{x_n=x_1 r^{n-1}}$$

将值代入方程，我们得到

$$\mathrm{1024=1×2^{n-1}}$$

$$\mathrm{1024=1×2^{n-1}}$$

我们可以将1024写成2¹⁰

$$\mathrm{2^{10}=2^{n-1}}$$

因为底数相同，所以我们可以将指数相等

$$\mathrm{10=n-1}$$

$$\mathrm{n=11}$$

因此，给定数列中有11项。

结论

数列是可以按一定顺序排列的一组数，数列中的元素可以以任何方式重复。算术数列是一个数列，其中每个元素的排列顺序使得该数列中每一项与前一项的差值相同。几何级数是一个数列，其中每个元素的排列顺序使得相邻两项的比值始终保持不变。

算术级数和几何级数的区别。

算术级数	几何级数
算术级数是一个数列，其中每个元素与前一项的差值相同。	几何级数是一个数列，其中数列中的每一项都是其前一项的倍数。
算术级数由相邻项之间的公差定义。	几何级数由相邻项之间的公比定义。
算术级数是一个线性数列	几何级数是一个指数数列。
算术级数示例：	几何级数示例： 10, 20, 40, 80,....
10, 30, 50, 70……

常见问题解答 (FAQ)

1. 列举代数中级数的类型。

代数中级数的类型包括：

• 算术级数 (AP)

• 几何级数 (GP)

• 调和级数 (HP)

2. 什么是调和级数？

它是构成算术级数的数字的倒数的数列。

3. 如何计算公比小于1的无穷级数？

具有无穷多项和公比小于1的几何级数可以通过以下公式计算：

$\mathrm{S=\frac{a}{1-r}}$，其中“a”是首项，“r”是公比。

4. 数列和级数有什么区别？

数列是基于定义属性的有序数字。例如2, 4, 6, 8……级数是有序排列的数字之和。例如2+4+6+8……

5. AP和HP之间有什么关系？

AP各项的倒数构成一个HP。