条形磁铁等效螺线管

---

引言

条形磁铁相当于一个螺线管。我们童年时都见过条形磁铁，并玩过它们。它具有吸引某些种类的材料的惊人特性。例如，它吸引铁，但对塑料表现出中性行为。条形磁铁由某种特殊的铁磁材料制成，它们具有永久磁性。

磁铁在当今的技术世界中非常有用。许多电子设备，如扬声器、硬盘驱动器和电视机都使用磁铁。我们知道，电流也能产生磁场。我们可以用电流产生类似条形磁铁的东西吗？答案是肯定的。在接下来的章节中，我们将看到线圈如何在某些配置下表现得像条形磁铁。它产生的磁场类似于条形磁铁，但也有一些区别。首先，我们将分别研究条形磁铁和螺线管，然后我们可以推导出表明它们产生类似磁场的方程式。

什么是条形磁铁？

条形磁铁是一块在其两端具有磁极的物质。它呈矩形，如图所示。

如果我们从中间将其自由悬挂，一端将指向地理北极，另一端将指向地理南极。一个称为北极，另一个称为南极。通常，这类磁铁是由铁、铝、镍等制成的。我们可以将其与静电学中的情况进行比较，其中两个电荷形成一个电偶极子。这里条形磁铁充当磁偶极子。

磁偶极子

假设m表示正磁荷（N极），-m表示负磁荷（S极），它们相距d。则

$$\mathrm{磁偶极矩\:\:\: \overrightarrow{\mu}=md}$$

方向是从-m到+m或从S到N。

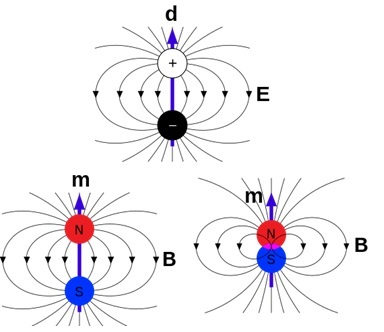
Maschen, Em dipoles, CC0 1.0

我们可以计算由此产生的磁场强度，在赤道位置的强度由下式给出：

$$\mathrm{\overrightarrow{B}=\frac{\mu_0}{4\pi}\frac{2\overrightarrow{\mu}}{r^2}………………. (i)}$$

什么是螺线管？

螺线管是一根长线，绕成线圈状。其长度与其直径相比非常大。

螺线管有什么用途？

它可以用作电磁铁。它们也可用于天线、电感器和断路器。

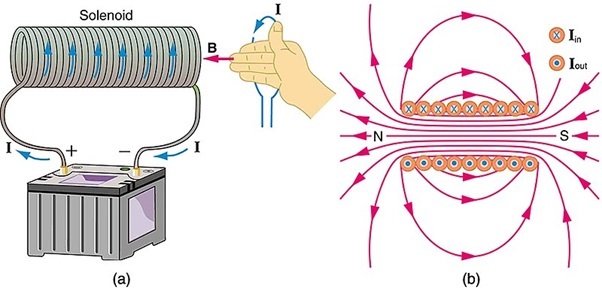
OpenStax, Openstax college-physics 22.40 solenoid-Bfield, CC BY 4.0

螺线管产生的磁场可以用安培环路定理计算。

如果n=单位长度的匝数，i是流过它的电流。

则

$$\mathrm{\overrightarrow{B}=\mu_0 n i(内部)}$$

条形磁铁等效螺线管的推导

首先，我们将计算载流环路在赤道点产生的磁场。我们取半径为'a'的圆形环路，导线中的电流设为i。假设在环路中心距离为d的点P处。我们想在这里计算由载流圆形环路产生的磁场。

让我们取一小段长度元dl，并计算它在P点产生的磁场。假设连接N和P的向量为$\mathrm{NP=\overrightarrow{r}}$

我们使用毕奥-萨伐尔定律

$$\mathrm{\overrightarrow{dB}=\frac{\mu_0}{4\pi}\frac{i\overrightarrow{dl}\times \overrightarrow{r}}{r^3}}$$

我们可以从图中看出$\mathrm{\overrightarrow{dl}}$垂直于图形平面，$\mathrm{\overrightarrow{dl}\times \overrightarrow{r}}$将在平面上。

$$\mathrm{I.e.\:\:\:\overrightarrow{dl}\times \overrightarrow{r}=dl \:r}$$

$$\mathrm{dB =\frac{\mu_0}{4\pi}\frac{idl}{r^2}}$$

我们可以使用图中的勾股定理计算

$$\mathrm{r^2= a^2+d^2}$$

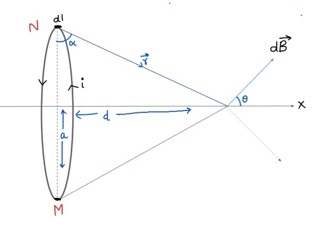
因此

$$\mathrm{dB =\frac{\mu_0}{4\pi}\frac{idl}{(a^2+d^2)}}$$

如果我们在M点取相同的元素，我们可以看到它将被分解为水平和垂直分量。其中M的垂直分量将抵消N的分量。因此，只有水平分量将起作用。如果我们将此逻辑扩展到整个环路的小元素，则只有水平分量将起作用。

一个元素的水平分量将是

$$\mathrm{dB_x = dB\:cosθ}$$

因此，由圆形环路产生的净场将是

$$\mathrm{B=\int dBcosθ=\int \frac{\mu_0}{4\pi}\frac{idl}{(a^2+d^2)}cosθ}$$

从图中

$$\mathrm{cosθ=\frac{a}{\sqrt{a^2+d^2}}}$$

$$\mathrm{B=\int \frac{\mu_0}{4\pi}\frac{idl}{(a^2+d^2)}\frac{a}{\sqrt{a^2+d^2}}=\frac{\mu_0}{4\pi}\frac{i}{(a^2+d^2)}\frac{a}{\sqrt{a^2+d^2}}\int dl=\frac{\mu_0}{4\pi}\frac{i}{(a^2+d^2)}\frac{a}{\sqrt{a^2+d^2}}2\pi a}$$

最终，

我们得到

$$\mathrm{B =\frac{\mu_0 i a^2}{2(a^2+d^2 )^{3/2}}……………………. (ii)}$$

螺线管作为条形磁铁

在公式(ii)中，如果我们考虑场点P远离线圈(d>>a)的情况

则

$$\mathrm{a^2+d^2\thickapprox d^2}$$

因此

$$\mathrm{B =\frac{\mu_0\:i\: a^2}{2d^3}=\frac{2\mu_0 (\Pi a^2)}{2\Pi 2d^3}}$$

我们知道载流导线的磁矩是$\mathrm{\overrightarrow{\mu}=iA=i\pi a^2}$

它给了我们

$$\mathrm{\overrightarrow{B}=\frac{\mu_0}{4\pi }\frac{2\overrightarrow{\mu}}{d^2}}$$

这个方程看起来很熟悉。它与公式(i)相同，公式(i)是由条形磁铁产生的磁场。因此，我们可以看到由许多这样的载流圆形环路组成的螺线管可以充当条形磁铁。

条形磁铁和螺线管的区别

这些是条形磁铁和螺线管的主要区别。

• 只有当电流流过螺线管时，它才能充当磁铁，然而，条形磁铁是永久磁铁。

• 条形磁铁的磁场强度是固定的，因此我们不能轻易改变它。但是我们可以通过增加或减少电流来改变螺线管的磁场。

• 条形磁铁的极性是固定的，但在螺线管的情况下，它可以改变。

条形磁铁和螺线管的相似之处

这些是条形磁铁和螺线管的相似之处。

• 在赤道点处的磁场对于条形磁铁和螺线管是相同的。

• 两者都放置在外加磁场中时会受到扭矩作用。

• 两者都具有吸引和排斥等磁性。

• 两者的磁力线方向相同。

螺线管如何像磁铁一样工作？

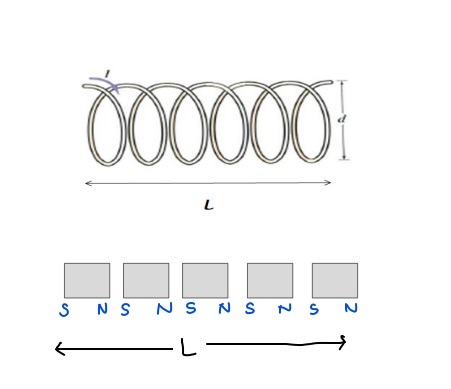
如果我们仔细观察螺线管，它类似于许多圆形环路的组合（如图所示）。如果电流i流过一个环路，则每个匝的磁矩等于iA。每个匝都可以被认为是一个小的磁偶极子，其磁矩μ=md。

如果我们使距离d非常接近，以至于一个的N极接触另一个的S极，依此类推。然后整个结构可以替换为只有一个北极和一个南极的条形磁铁。

结论

载流导线在赤道点产生一个磁场，该磁场可以等于磁偶极子产生的电流。为此，计算磁场的点与线圈半径相比应非常大。螺线管可以建模为多个平行线圈，它们之间的距离非常近。因此它可以作为条形磁铁。它们是相似的，因为它们产生相似的磁场，但它们是不同的，因为一个是永久磁铁，另一个是电磁铁。

常见问题

Q1. 电偶极子和磁偶极子的区别是什么？

A1. 电偶极子由两个实体组成，即正电荷和负电荷，它们是存在的。但是，不可能存在独立的北极或南极。它们总是成对出现的。

Q2. 磁铁有多少种类型？

A2. 一般来说，磁铁有三种类型：永久磁铁、临时磁铁和电磁铁。

Q3. 螺线管外部产生的磁场强度是多少？

A3. 螺线管外部的磁场强度为零，因为那里的电流为零。

Q4. 我们能否使用安培环路定理来计算圆形导线在赤道点产生的磁场？

A4. 不行，它只能应用于高度对称的情况。

Q5. 条形磁铁如何在没有电流的情况下产生磁场？

A5. 在微观层面上，运动的电子在原子层面上产生电流。在磁铁中，这些小的电流环路是平行排列的，因此它们不会相互抵消。