数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会科学
时装研究
法律研究在不生成树的情况下检查相同的二叉搜索树（英语）
有两个数组来表示二叉搜索树的元素。如果从左至右从数组中提取元素，并形成二叉搜索树，那么通过从两个数组中提取，将会形成同一棵二叉搜索树。必须检查是否两者形成的相同。但是约束条件是无法形成二叉搜索树。假设两个数组分别为 {2, 4, 1, 3} 和 {2, 1, 4, 3}，如果观察一下，这两个序列都可以形成相同的二叉搜索树。
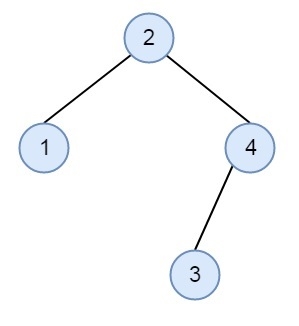
方法很简单。众所周知，左子树的元素小于根节点，右子树的元素大于根节点。如果对于每个元素 x，x 的左子树和右子树中的元素在两个数组中都出现在它的后面，那么这两个列表可以表示相同的二叉搜索树。左子树和右子树的根节点也是如此。将检查在两个数组中较小的下一个元素和较大的下一个元素是否相同。对于左子树和右子树，相同的方式进行递归检查。
示例
#include <iostream>
using namespace std;
bool isSameCheckHelper(int tree1[], int tree2[], int n, int i1, int i2, int min, int max) {
int j, k;
for (j = i1; j < n; j++)
if (tree1[j] > min && tree1[j] < max)
break;
for (k = i2; k < n; k++)
if (tree2[k] > min && tree2[k] < max)
break;
if (j==n && k==n) //If the parent element is leaf in both arrays
return true;
if (((j==n)^(k==n)) || tree1[j]!=tree2[k])
return false;
return isSameCheckHelper(tree1, tree2, n, j+1, k+1, tree1[j], max) &&
// for Right Subtree
isSameCheckHelper(tree1, tree2, n, j+1, k+1, min, tree1[j]); // for Left Subtree
}
bool areBSTSame(int first[], int second[], int n) {
return isSameCheckHelper(first, second, n, 0, 0, INT_MIN, INT_MAX);
}
int main() {
int first[] = {8, 3, 6, 1, 4, 7, 10, 14, 13};
int second[] = {8, 10, 14, 3, 6, 4, 1, 7, 13};
int n=sizeof(first)/sizeof(first[0]);
if(areBSTSame(first, second, n)) {
cout << "Two BSTs are same";
} else {
cout << "Two BSTs are not same";
}
}输出
Two BSTs are same
更新于：2019 年 10 月 21 日
87 次浏览
广告