真空介电常数

---

介绍

介电常数是一个关键概念，应用于电学领域。不同的材料具有保持大量电荷较长时间的特性。材料的这种特性称为介电性。

什么是介电材料？

介电材料是一种导电性差但能够储存电荷的材料。许多材料都是介电材料，例如真空、金属、空气或水。在电路中增加电容，介电材料起着重要作用。

什么是介电常数？

介电常数衡量介电材料在电场中储存能量的能力。它也称为相对介电常数。

• 它定义为材料的介电常数与自由空间介电常数的比率。

• 它也解释了由于电场强度在电场中某点产生的磁通密度。

介电常数公式

介电常数的数学表达式如下：

$$\mathrm{K=\frac{\epsilon}{\epsilon_0}}$$

其中K是介电常数

$\mathrm{\epsilon}$是材料的介电常数

$\mathrm{\epsilon_o}$是自由空间的介电常数

介电常数单位

因为它是由两个相同量纲的量相除得到的，所以它没有单位和量纲。

介电常数符号

比诱电常数，即介电常数，用希腊字母Kappa，K表示。

介电常数背后的理论

它是指定电容器所需的主要变量。电容器是一种用于储存电荷的电子器件，它是由将介电绝缘板置于金属导电板之间形成的。

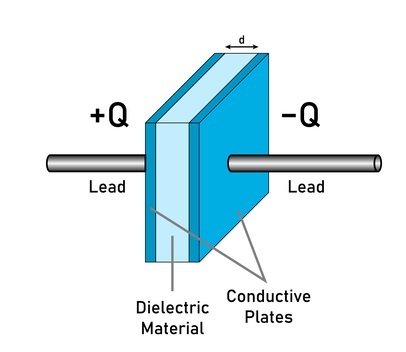
• 这种介电材料层决定了电容器储存电荷的效率和容量。因此，建议选择最佳的介电材料。

• 介电材料的这种特性在电容器的工作中非常重要。

• 介电常数也可以解释为无介电材料的电场$\mathrm{(E_0)}$与有介电材料的电场(E)的比率。

$$\mathrm{K=\frac{E_0}{E}}$$

• $\mathrm{E_0}$总是大于或等于E。因此，介电常数K的值总是大于1。

• K的值越大，电容器储存的电荷就越多。

• 带有介电材料的电容器的电容C和没有介电材料的电容器的电容$\mathrm{C_0}$之间的关系是

$$\mathrm{C=KC_0}$$

因此，如果在电容器极板之间的空间填充介电材料，则其电容值将增加介电常数值。

平行板电容器的电容公式为

$$\mathrm{C=\frac{K \varepsilon_0A}{d}}$$

这里：

• C表示平行板电容器的电容

• K表示介电常数

• $\mathrm{\varepsilon_0}$表示自由空间的介电常数

• A表示平行板电容器的面积

• d是平行板之间的距离

从上述表达式可以看出，可以通过提高介电常数值和减小平行板之间的距离来增加电容。

介电常数值

不同介电材料的介电常数值不同，如下所示：

序号	介电材料	介电常数值
1	特氟龙	2.1
2	混凝土	4.5
3	空气	1.00059
4	真空	1
5	水	80
6	硅	11.68
7	金刚石	5.5 - 10

表1：不同介电材料的介电常数

影响介电常数的因素

影响介电常数值的因素如下：

温度

在低温下，介电材料分子的调整比较困难。但是，如果温度升高，材料的偶极矩会增加，从而增加介电常数值。介电常数开始增加的温度称为转变温度。如果温度升高到转变温度以上，则介电常数会持续下降。

频率

如果外部电压的频率增加，介电常数值将变得非线性。

施加电压

如果供给交流电压，则介电常数值将增加，而如果供给直流电压，则其值将减小。

湿度

随着湿度增加，介电常数值减小。

加热效应

如果介电材料被加热，材料中的分子会运动，导致能量耗散，这被认为是介电损耗。当介电材料提供电能时，这种以热量形式的损耗就会发生。

结构和形态

介电常数受材料的结构和形态影响。

结论

本教程简要介绍了介电常数，它也被称为相对介电常数的历史术语。对于零频率，材料的介电常数被认为是静态或基于频率的变量。

此外，本教程还简要介绍了影响介电常数的因素。本教程中说明了该常数相对于几个物理量的不同表达式。本教程可能有助于理解不同介电材料的介电常数。

常见问题

Q1. 你对介电材料的极化有什么理解？

A1. 当施加外部电场时，在介电材料中产生电偶极子；这个过程称为介电材料的极化。

Q2. 解释相对介电常数如何影响环境。

A2. 当湿度、温度和气压发生变化时，大气中的空气会受到影响，从而影响相对介电常数，进而改变电容值。借助传感器，可以测量这些变化。

Q3. 定义离子极化。

A3. 当施加外部电场时，正离子或负离子向相反方向移动的过程称为离子极化。

Q4. 铁电材料是什么意思？

A4. 当不施加外部电场时，显示电子极化的材料称为铁电材料。例如，钛酸钡$\mathrm{(BaTiO_3)}$和磷酸二氢钾$\mathrm{(KH_2 PO_4)}$

Q5. 如果将电容器放在真空中，极板的横截面积为$\mathrm{6m^{2}}$，极板之间的距离为3m。计算电容器的电容。$\mathrm{(\varepsilon_0=8.85\times 10^{−12}Fm^{−1})}$

A5. 已知

极板横截面积=$\mathrm{6m^{2}}$

极板之间的距离=3m

电容器置于真空中，K=1

$$\mathrm{(\varepsilon_0=8.85\times 10^{−12}Fm^{−1})}$$

电容器的电容，$\mathrm{C=\frac{K \varepsilon_0 A}{d}}$

$$\mathrm{C=\frac{1\times 8.85\times 10^{−12}\times 6}{3}}$$

$$\mathrm{C=17.7\times 10^{−12}F}$$

Q6. 定义介电材料的损耗角正切。

A6. 由于导电、介电谐振和弛豫等多种物理过程，材料中存在能量耗散，这被称为介电损耗角正切，用$\mathrm{tan \delta}$表示。