DBMS 中可能的超级键数量

---

在数据库管理系统 (DBMS) 中，超级键是用于识别表中唯一记录的重要概念。超级键是一组一个或多个属性，可以唯一地识别表中的一条记录。

在本文中，我们将探讨数据库中可能的超级键数量及其意义。

什么是超级键？

超级键是表中的一组属性，可以唯一地识别该表中的每一行。它与主键和候选键不同，因为只有最小的可能的超级键才能被选为主键或候选键。因此，主键或候选键是没有不必要属性的超级键。所有主键或候选键都是超级键，但并非所有超级键都是主键或候选键。表的定义规定所有行都是唯一的，因此所有属性的集合本身就是一个超级键。

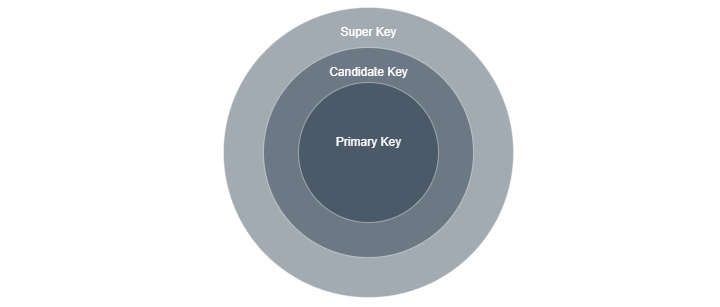
例如，如果我们有一个包含以下列的学生表：学生 ID、姓名和电子邮件。这里，学生 ID 和姓名的组合可以形成一个超级键。此外，学生 ID、姓名和电子邮件也可以形成一个超级键。

我们将在这里使用包含-排除的各种属性。

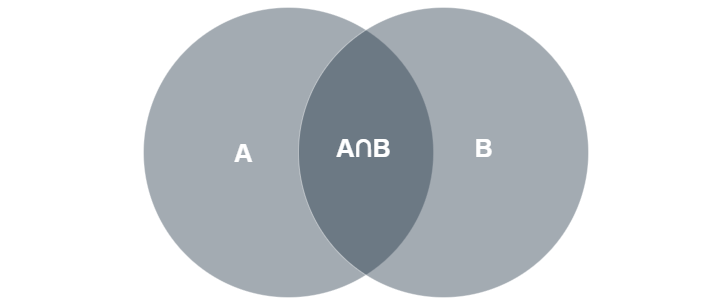
计算 DBMS 中可能的超级键数量

示例-1

假设我们有一个具有属性 {a1, a2, a3} 的关系 R，并且 a1 是候选键。那么，a1 的任何超集都是超级键。因此，我们可以有四个可能的超级键：{a1, a1 a2, a1 a3, a1 a2 a3}。一般来说，如果我们有 'N' 个属性和一个候选键，则可能的超级键数量为 2^(N – 1)。

示例-2

假设我们有一个具有属性 {a1, a2, a3,…,an} 的关系 R。超级键的最大数量为 2^(n) – 1。要成为超级键，必须至少存在一个属性；空集或没有属性的集合不能是超级键。

示例-3

假设我们有一个具有属性 {a1, a2, a3,…, an} 的关系 R，并且候选键为“a1 a2 a3”。根据之前的公式，我们有三个属性而不是一个。因此，这里可能的超级键数量为 2^(N-3)。

示例-4

假设我们有一个具有属性 {a1, a2, a3,…, an} 的关系 R，并且候选键为“a1”，“a2”。在这种情况下，我们有两个不同的候选键，而不仅仅是一个。我们可以使用以下公式

可能的超级键

= (使用候选键 A1 可能的超级键) + (使用候选键 A2 可能的超级键) – (来自 A1 和 A2 的公共超级键)。

= = 2^(n-1) + 2^(n-1) - 2^(n-2)

示例-5

假设我们有一个具有属性 {a1, a2, a3,…, an} 的关系 R，并且候选键为“a1”，“a2 a3”。我们可以使用以下公式

= (a1) 的超级键 + (a2 a3) 的超级键 – (a1 a2 a3) 的超级键。

= 2^(n - 1) + 2^(n - 2) - 2^(n - 3)

示例-6

假设我们有一个具有属性 {a1, a2, a3,…, an} 的关系 R，并且候选键为“a1 a2”，“a3 a4”。我们可以使用以下公式

= (a1 a2) 的超级键 + (a3 a4) 的超级键 – (a1 a2 a3 a4) 的超级键。

= 2^(n - 2) + 2^(n - 2) - 2^(n - 4)

示例-7

假设我们有一个具有属性 {a1, a2, a3,…, an} 的关系 R，并且候选键为“a1 a2”，“a1 a3”。我们可以使用以下公式

= (a1 a2) 的超级键 + (a1 a3) 的超级键 – (a1 a2 a3) 的超级键。

= 2^(n - 2) + 2^(n - 2) - 2^(n - 3)

示例-8

假设有一个具有属性 {a1, a2, a3,…,an} 的关系 R。如果候选键为“a1”，“a2”和“a3”，则可能的超级键有多少个？

要找出超级键的数量，我们可以使用下图所示的公式。我们只需要将关系中的属性数量 (n) 和我们拥有的候选键数量代入即可。

公式为

|A1 ∪ A2 ∪ A3| = |A1| + |A2| + |A3| – |A1 ∩ A2| – |A1 ∩ A3| – |A2 ∩ A3| + |A1 ∩ A2 ∩ A3|

= (使用候选键 A1 可能的超级键) + (使用候选键 A2 可能的超级键) + (使用候选键 A3 可能的超级键) – (来自 A1 和 A2 的公共超级键) – (来自 A1 和 A3 的公共超级键) – (来自 A2 和 A3 的公共超级键) + (来自 A1、A2 和 A3 的公共超级键)

= 2^(n-1) + 2^(n-1) + 2^(n-1) – 2^(n-2) – 2^(n-2) – 2^(n-2) + 2^(n-3)

示例-9

假设有一个关系 R (A, B, C, D, E, F, G, H)，并且函数依赖集为 CH → G、A → BC、B → CFH 和 E → A、F → EG。存在多少个可能的超级键？

首先，我们需要找出候选键，它们是 AD、BD、ED 和 FD。然后我们需要找到由于单个候选键、两个候选键的组合、三个候选键和所有候选键而产生的可能的超级键。应用包含-排除原理后，我们可以找到超级键的数量，即 120。

示例-10

假设有一个具有属性 {a1, a2, a3…an} 的关系 R，并且 {a1a2a3…ak} 作为候选键，其中 k<=n。可能的超级键有多少个？

可能的超级键数量为 2^(n-k)。

示例-11

假设有一个具有属性 {a1, a2, a3…an} 的关系 R，使得任何 k 个属性一次确定所有其他属性。我们需要找到 k 的值，使得关系中的候选键数量最大。

任何 k 个属性一次构成一个候选键。这些 k 个属性是从 n 个属性中随机选择的。因此，对于某个 k，可能的候选键数量为 nCk，即 n!/(n-k)!k!。为了使候选键的数量最大化，k 必须为 ⌊n/2⌋，以便 nCk 为该值的最大值。