电流、电压和电阻概述 电流

电荷（自由电子）的有向流动称为电流。换句话说，电流定义为电荷（自由电子）流动的速率。它用𝐼 或 𝑖表示，以安培(A)为单位测量，即：

$$I=\frac{Q}{t}=\frac{ne}{t}\:\:安培(A)$$

其中，Q = ne，e = 1.6 X 10^-19 C。

微分形式为：

$$i=\frac{dq}{dt}$$

电流是如何流动的？

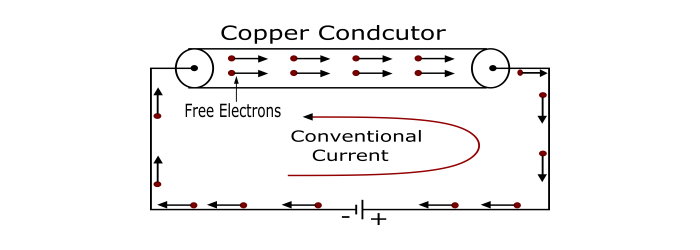
如图所示，铜导体含有大量自由电子。当在其两端施加电位差（电压）时，自由电子（带负电）开始向电源的正极移动。这种定向流动的自由电子称为电流。

实际电流（或电子电流）的方向是从负极通过外部电路到正极。但在电子理论出现之前，人们认为电流是正电荷从正极通过外部电路到负极的流动。因此，这种假设的电流方向被称为常规电流。

电流类型

电流可分为三种类型：

• 稳态电流

• 变化电流

• 交流电

稳态电流

大小不随时间变化的电流称为稳态电流（直流电）。电池提供的电流就是稳态电流的一个例子。

变化电流

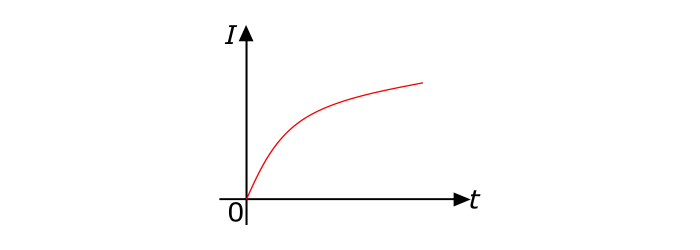
大小随时间连续变化的电流称为变化电流。指数变化的电流（如电感中的电流）就是变化电流的一个例子。

交流电

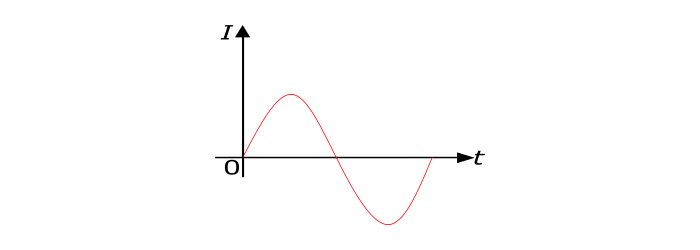
大小随时间连续变化且方向周期性变化的电流称为交流电。由于这种电流在电路中交替流动，即在半个周期内沿一个方向流动，在另一个半个周期内沿相反方向流动，因此被称为交流电。

电势

当一个物体带电时，充电过程中会做功。这项功以势能的形式储存在物体中。现在，这个带电物体能够通过吸引或排斥来移动其他电荷。因此，它具有做功的能力，这被称为物体的电势，即：

带电物体做功的能力称为该物体的电势。电势的量度是所做功 (W) 与电荷 (Q) 的比值，即：

$$电势(V)=\frac{所做功(W)}{电荷(Q)}$$

所做功以焦耳为单位测量，电荷以库仑为单位测量，因此电势的单位是焦耳/库仑或伏特。

电位差或电压

两个带电体的电势差称为电位差。

电位差也称为电压。因此，不存在单点电压，即必须使用某个参考点作为另一个点。

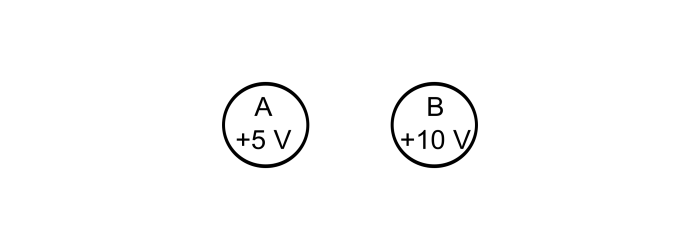
如果两个物体具有不同的电势，则它们之间存在电位差。考虑上图所示的两个物体，物体 A 的电势为 5 V，这意味着物体 A 的每个库仑电荷具有 5 焦耳的能量，而物体 B 的电势为 10 V，这意味着物体 B 上的每个库仑电荷具有 10 焦耳的能量。

如果这两个物体通过导线连接，则电流（常规电流）将从高电势流向低电势，即从物体 B 流向物体 A。当这两个物体达到相同的电势时，电流将停止流动。因此，可以说，如果存在电位差，则电流将在电路中流动。无电压，无电流。

电阻

物质对电流（电子）流动所提供的阻碍程度称为其电阻。它以欧姆 (Ω) 为单位测量。电阻的电路符号如下所示。

由于电流是电子的流动，因此电阻是物质对这些电子流动所提供的阻碍。由于电阻是物质提供的电阻，因此它会导致电流流动时产生热量。

影响电阻的因素

• 导体的电阻与其长度 (𝑙) 成正比。

• 导体的电阻与其横截面积 (a) 成反比。

• 电阻取决于导体材料的性质。

• 电阻随温度变化而变化。

因此，根据前三点，我们得到：

$$R\propto\frac{l}{a}$$

$$R=\rho\frac{l}{a}$$

其中，ρ（Rho）是一个常数，称为电阻率或比电阻。其值取决于材料的性质。ρ 的单位为欧姆·米 (Ω·m)。

温度对电阻的影响

• **纯金属（导体）** – 铜、铝等纯金属的电阻随温度升高而增加。纯金属的温度/电阻曲线是一条直线。由于纯金属的电阻随温度升高而增加，因此它们具有正温度电阻系数。

• **绝缘体、半导体和电解质** – 这些材料的电阻随温度升高而降低。因此，这些材料具有负温度电阻系数。

• **合金** – 合金的电阻随温度升高而增加，但这种增加很小且不规则，在很宽的温度范围内实际上可以忽略不计。

数值示例 #1

当 2.56 X 10¹⁷ 个电子在 65 毫秒内通过导体时，求导体中的电流。

解答

$$电流(I)=\frac{Q}{t}=\frac{ne}{t}=\frac{(2.56\times\:10^{17})\times\:(1.6\times\:10^{-19})}{65\times\:10^{-3}}$$

$$=630\times\:10^{-3}A=630mA$$

数值示例 #2

电池的电压为 12 V。它需要输送多少电荷才能做 60 J 的功。

解答

$$输送电荷(Q)=\frac{W}{V}=\frac{60}{12}=5C$$

数值示例 #3

计算 500 米长的导线的电阻，其均匀横截面积为 0.69 cm²。该导线由电阻率为 1.7 × 10^-6Ω·cm 的铜制成。

解答

$$R=\rho\frac{l}{a}=(1.7\times\:10^{-6})\times\:\frac{500}{0.69\times\:10^{-4}}=12.32\Omega$$

Saini Manish Kumar

更新于：2021年5月29日

917 次查看

启动您的职业生涯

完成课程获得认证

开始学习