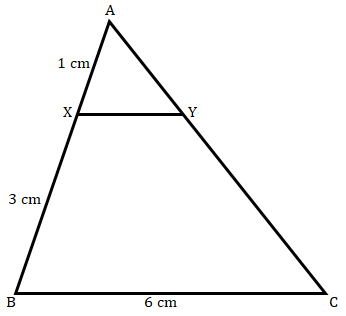
In figure below, $XY\ ∥\ BC$. Find the length of $XY$.
"\n

Problem Statement

In figure below, $XY\ ∥\ BC$. Find the length of $XY$.

Solution

Given:

In the given figure $XY\ ∥\ BC$.

To do:

We have to find the length of $XY$.

Solution:

$AX = 1\ cm, BX = 3\ cm$ and $BC = 6\ cm$

In $\vartriangle AXY$ and $\vartriangle ABC$,

$\angle A = \angle A$  (Common)

$\angle AXY = \angle ABC$ ($XY||BC$, Corresponding angles)

Therefore,

$\vartriangle AXY ∼ \vartriangle ABC$   (By AA similarity)

Hence,

$\frac{XY}{BC} = \frac{AX}{AB}$ (Corresponding parts of similar triangles are

proportional)

$\frac{XY}{6} = \frac{1}{1+3}$        ($AB=AX+BX=(1+3)\ cm$)

$XY = \frac{6\times1}{4}$

$XY = 1.5\ cm$

The length of $XY$ is $1.5\ cm$.

Tutorialspoint

Updated on: 10-Oct-2022

40 Views

Kickstart Your Career

Get certified by completing the course

Get Started