数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究函数依赖集的等价是什么？
如果函数依赖 (FD) 集 F 的闭包中包含 E 中的每个 FD，则称函数依赖集 (FD) F 覆盖另一个函数依赖集 E；也就是说，如果可以从 F 推导出 E 中的每个依赖项。
或者，我们可以说 E 被 F 覆盖。如果 E+= F+，则两个函数依赖集 E 和 F 等价。也就是说，如果 E 覆盖 F 且 F 覆盖 E，则 E 等价于 F。
为了确定 F 是否覆盖 E，我们针对 E 中的每个 FD X->y 计算 F 相对于 X 的闭包 X+，然后检查 X+ 是否包含属性 Y。
示例
R=(A,B,C,D,E,F)
F1={A->BC, B->CDE, AE->F}
F2={A->BCF, B->DE, E->AB}
检查 F1 和 F2 是否等价。
解决方案
检查 F1 是否覆盖 F2 -
A+={A,B,C,D,E,F} 包含 B,C,F
B+={B,C,D,E} 包含 D,E
E+={E} 包含 A,B
所以 F1 不覆盖 F2。
因此，F1 和 F2 不等价。
示例
考虑另一个两个函数依赖等价的示例。
R=(A,C,D,E,H)
F1={A->C, AC->D, E->AD, E->H},
F2={A->CD, E->AH}
检查 F1 和 F2 是否等价？
解决方案
检查 F1 是否覆盖 F2 -
A+={A,C,D} 包含 C,D
E+={A,D,E,H} 包含 A,H
所以 F1 覆盖 F2
检查 F2 是否覆盖 F1
A+={A,C,D} 包含 C
{ A,C}+={A,C,D} 包含 D
E+={A,C,D,E,H} 包含 A,D,H
所以 F2 覆盖 F1。
因此，F1 和 F2 等价。
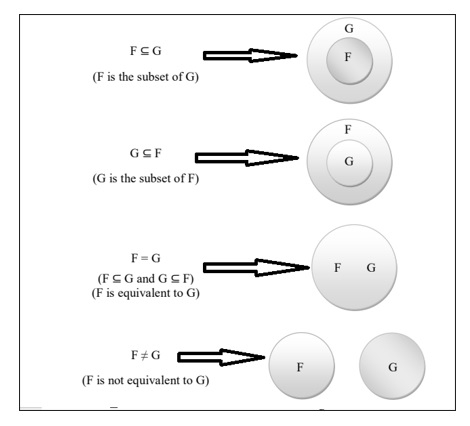
这可以用图表表示如下 -
更新于： 2021年7月3日
6K+ 次查看
广告