- Excel 函数教程
- Excel 函数 - 首页
- 兼容性函数
- 逻辑函数
- 文本函数
- 日期和时间函数
- 多维数据集函数
- 数学函数
- 三角函数
- 数据库函数
- 动态数组函数
- 工程函数
- 财务函数
- 信息函数
- 查找和引用函数
- 统计函数
- 网络函数
- Excel 有用资源
- Excel - 快速指南
- Excel - 有用资源
- Excel - 讨论
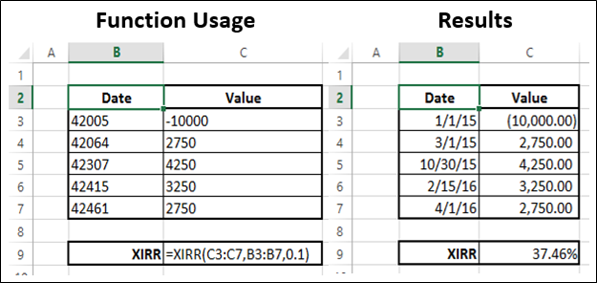
Excel - XIRR 函数
描述
XIRR 函数返回非周期性现金流计划的内部收益率。要计算一系列周期性现金流的内部收益率,请使用 IRR 函数。
语法
XIRR (values, dates, [guess])
参数
| 参数 | 描述 | 必填/可选 |
|---|---|---|
| 值 | 与支付日期计划相对应的现金流系列。 参见下面的注释。 |
必填 |
| 日期 | 与现金流支付相对应的支付日期计划。 日期可以按任意顺序排列。 参见下面的注释。 |
必填 |
| 猜测值 | 您猜测接近 XIRR 结果的数字。 | 可选 |
注释
第一次支付是可选的,对应于投资开始时的成本或支付
如果第一个值是成本或支付,则它必须为负值
所有后续支付均基于 365 天的年度进行折现
值序列必须至少包含一个正值和一个负值。日期应使用 DATE 函数输入,或作为其他公式或函数的结果输入。如果日期作为文本输入,则可能会出现问题。
Microsoft Excel 将日期存储为连续序列号,以便可在计算中使用它们。默认情况下,1900 年 1 月 1 日是序列号 1,2008 年 1 月 1 日是序列号 39448,因为它是 1900 年 1 月 1 日之后的第 39,448 天。
日期中的数字将截断为整数。
XIRR 至少需要一个正现金流和一个负现金流。否则,XIRR 将返回 #NUM! 错误值。
如果日期中的任何数字不是有效的 Excel 日期,则 XIRR 将返回 #VALUE! 错误值。
如果日期中的任何数字早于起始日期,则 XIRR 将返回 #NUM! 错误值。
如果值和日期包含不同数量的值,则 XIRR 将返回 #NUM! 错误值。
在大多数情况下,您不需要为 XIRR 计算提供猜测值。如果省略,则假设猜测值为 0.1(10%)。
XIRR 与净现值函数 XNPV 密切相关。XIRR 计算的收益率是对应于 XNPV = 0 的利率。
Excel 使用迭代技术来计算 XIRR。使用变化的利率(从猜测值开始),XIRR 将循环执行计算,直到结果精确到 0.000001% 以内。如果 XIRR 在 100 次尝试后仍找不到有效的结果,则将返回 #NUM! 错误值。利率将发生变化,直到:
$$0 = \sum_{i=1}^{N} \frac{P_i}{\left ( 1 + rate \right )^{\frac{\left ( d_i - d_1 \right )}{365}}}$$
其中:
di = 第 i 次(或最后一次)支付日期。
d1 = 第 0 次支付日期。
Pi = 第 i 次(或最后一次)支付。
适用性
Excel 2007、Excel 2010、Excel 2013、Excel 2016
示例