环形

---

简介

环形（复数为 annuli 或 annuluses）两个同心圆之间的区域。名称“环形”源自拉丁词 annulus 或 annulus，意思是“小环”。Annular 是形容词形式（如环形日食）。开放环形和穿孔平面在拓扑上彼此相等。环形是两个同心圆或具有两个以上旋转中心的圆之间的内部空间。本文将向您介绍环形的多种数学用途，它具有环状形状。日常生活中的例子包括指环、甜甜圈等。为了更好地理解这个概念，让我们进一步研究环形的形状，并通过一些例子进行练习。

环形：圆形环（定义）

• 环形是一种二维平面图形，具有圆形形状，由两个同心圆组成。

• 环形是这两个同心环之间形成的区域或面积。由于它是一个具有圆形的平面图形，因此边缘是两个具有相同中心的圆。

• 由于物体的中心有一个圆，因此它看起来像一个圆盘。

• 单词“环形”源自拉丁语“annuli”，意思是“小环”。

• 环形类似于投掷环或圆盘，因为它扁平且圆形，中间有一个孔。

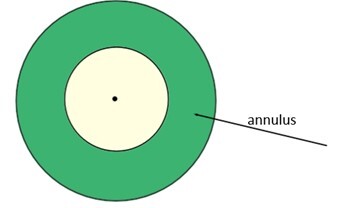
• 请查看下面的插图，其中有两个圆——一个小圆，也称为内圆，一个大圆，通常称为外圆。这两个圆的中心都位于黑色标记的位置。环形是这两个圆边缘之间呈绿色的区域。

周长和面积

• 二维形状的周

• 长是围绕它的空间。环形也可以称为环，因为它是由两个同心圆组成的扁平圆形。因此，穿孔平面和圆柱体可以被认为是开放环的拓扑等价物。与面积类似，为了获得环形的周长，我们必须考虑内圆和外圆。然后，通过将大和小的圆的半径相加并乘以 2 来确定环或环形的周长。使用以下公式计算周长：

  $$\mathrm{环形周长=2π(R+r)}$$

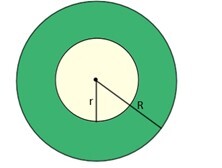
  其中 R 是外环的半径，r 是小环的半径。

• 环形区域是指环形空间的面积，或两个同心圆之间的封闭区域。为了确定环形的面积，我们必须知道内圆和外圆的面积。环形的尺寸由两个半径 R 和 r 定义，分别对应于外环和内环的半径。当我们知道这两个半径的尺寸时，我们可以通过从大圆的面积中减去小圆的面积来计算面积。因此，使用以下公式确定环形的面积：

  $$\mathrm{环形面积=π(R^2-r^2)}$$

  其中 R 是外环的半径，r 是小环的半径。

解题示例

1)如果环形的外半径为 12 个单位，内半径为 6 个单位，则计算其面积。

答案

已知

$$\mathrm{R=12\: \&\: r=6}$$

因此，使用环形面积公式，我们得到；

$$\mathrm{环形面积=π(R^2-r^2 )}$$

$$\mathrm{=π(12^2-6^2 )}$$

$$\mathrm{=π(144-36)=108π\: 平方单位}$$

2)如果外半径为 14 个单位，内半径为 9 个单位，则计算环形的周长。

答案

已知

$$\mathrm{R=14\: \&\: r=9}$$

因此，使用环形周长公式，我们得到；

$$\mathrm{环形周长=2π(R+r)=2π(14+9)=2π(23)=46π\: 单位}$$

3)钢管横截面的面积是多少，其外半径为 100 个单位，内半径为 50 个单位？

答案

已知

$$\mathrm{R=100\: \&\: r=50}$$

因此，使用环形面积公式，我们得到；

$$\mathrm{环形面积=π(R^2-r^2)=π(100^2-50^2)=π(150)(50)=7500π\: 平方单位}$$

因此，钢管横截面的面积为 7500π 平方单位

4)求周长为 18π 且外半径为 7 厘米的环形的内半径。

答案

已知

$$\mathrm{R=7\: \&\: r=?}$$

因此，使用环形周长公式，我们得到；

$$\mathrm{环形周长=2π(R+r)=2π(7+r)}$$

$$\mathrm{18π=2π(7+r)}$$

$$\mathrm{\frac{18}{2}=r+7}$$

$$\mathrm{r=9-7=2}$$

因此，内圆的半径为 2 厘米。

5)DVD 光盘的面积是多少，其外半径为 100 个单位，内半径为 50 个单位？

答案

已知

$$\mathrm{R=100\: \&\: r=50}$$

因此，使用环形面积公式，我们得到；

环形面积=π(R²-r²)=π(100²-50²)=π(150)(50)=7500π 平方单位。因此，DVD 光盘的面积为 7500π

6)如果环形的外半径为 14 个单位，内半径为 7 个单位，则计算其面积。

答案

已知

$$\mathrm{R=14\: \&\: r=7}$$

因此，使用环形面积公式，我们得到；

环形面积=π(R²-r²)=π(14²-7²)=π(196-49)=147π 平方单位

7)求周长为 20π 且外半径为 8 厘米的环形的内半径。

答案

已知

$$\mathrm{R=8\: \&\: r=?}$$

因此，使用环形周长公式，我们得到；

$$\mathrm{环形周长=2π(R+r)=2π(8+r)}$$

$$\mathrm{20π=2π(8+r)}$$

$$\mathrm{\frac{20}{2}=r+8}$$

$$\mathrm{r=10-8=2}$$

因此，内圆的半径为 2 厘米。

结论

• 环形是一种二维平面图形，具有圆形形状，由两个同心圆组成。环形是这两个同心圆之间形成的区域或面积。

• 环形面积=π(R²-r²)，其中 R 是外环的半径，r 是小环的半径。

• 环形周长=2π(R+r)，其中 R 是外环的半径，r 是小环的半径。

常见问题

1. 环形有几条边？

环形是一种类似于环的平面形状。它有两个具有相同中心的圆作为其边缘。环形物体是指具有环形形状的物体。

2. 环形的定义是什么？

环形是由两个圆连接而成的形状。环形是由两个同心圆（共享一个共同中心的圆）的交点形成的平面图形。环形具有环的形状。

3. 环形是圆的哪一部分？

环形是两个圆的外边缘之间的空间。两个圆的外边缘之间的区域始终类似于中间有一个孔的圆。两个同心圆的差形成一个环形。

4. 环形可以是正方形吗？

根据切片方式，环形可以解释为闭合弦单点函数的平方或开放弦双点函数。

5. 什么是环形表面？

环形表面是由圆组成的单一曲率线系统组成的表面。考虑接触两个连续表面球体的球体：这些球体形成一个特殊的线性同余；它们必须接触球体。