数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++中的Bellman-Ford算法？
Bellman-Ford算法是一种动态规划算法，用于查找从作为起始顶点的某个顶点计算的任何顶点的最短路径。该算法采用迭代方法，并不断尝试查找最短路径。Bellman-Ford算法应用于加权图。
该算法由Alphonso Shimbel于1955年提出。由于Richard Bellman和Lester Ford在1956年和1958年对算法进行了修改，因此该算法被命名为**Bellman-Ford算法**。Eward F. Moore也在1957年对该算法进行了修改，这使得该算法也被称为**Bellman-Ford-Moore算法**。
该算法的优势在于它可以处理具有负权边的图。尽管该算法比Dijkstra算法慢，但它能够处理更通用的图类型，因此更强大。
算法
Input : weighted graph and starting vertex Output : shortest distance between all vertices from the src. For negative weight cycle, the same will be returned as the weight cannot be calculated.
算法
Step 1 : This is the initialisation step, an array is created that stores the distance of all vertices from the initial vertex. The array say dist[] of size equal to the number of vertices in the graph. Step 2 : Calculate the shortest distance of vertex. Loop through step 3 for n-1 number of times ( n is the number of vertices of graph). Step 3 : Follow following steps for each edge i-j Step 3.1 : If dist[v] > dist[u] + weight[uv]. Then, dist[v] = dist[u] + weight[uv]. Step 4 : Check and flag if there is any negative cycle. If step 3.1 executes then there is a negative cycle.
负环：如果存在一条路径比常规边遍历更短，则存在负环。
示例
让我们通过解决一些与图相关的难题来了解更多关于该算法的信息。
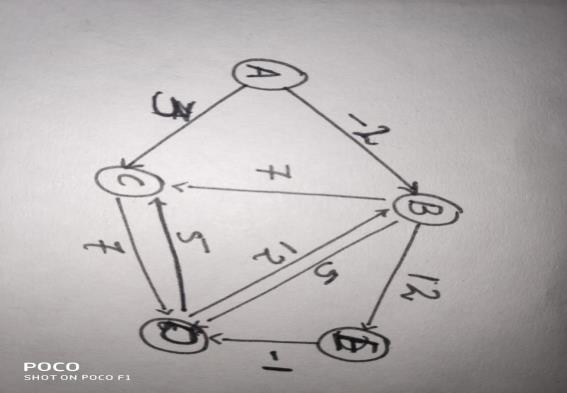
您可以看到图的所有顶点和边以及它们关联的权重。
让我们使用Bellman-Ford算法查找**顶点A和顶点E**之间的最短距离。
将源顶点(A)设置为零0，并将其余距离设置为无穷大∞。
A B C D E 0 ∞ ∞ ∞ ∞
检查边**A-B**然后**A-C**的权重，
对于A-B，我们只有一条路径，但对于A-C，我们有两条可以遍历的路径，我们将检查哪一条最短。
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ - for (A-B) 0 -2 3 ∞ ∞ - for (A-C)
对于接下来的顶点，我们将计算初始顶点的最短距离。
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ 0 -2 3 3 10
因此，使用该算法的最短距离是10。遍历路径**A-B-E**。使用此方法，我们还发现存在负环。
示例
#include <bits/stdc++.h>
struct Edge {
int src, dest, weight;
};
struct Graph {
int V, E;
struct Edge* edge;
};
struct Graph* createGraph(int V, int E) {
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
void BellmanFord(struct Graph* graph, int src) {
int V = graph->V;
int E = graph->E;
int dist[V];
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v]) {
printf("Graph contains negative weight cycle");
return;
}
}
printf("Vertex :\t\t\t ");
for (int i = 0; i < V; ++i)
printf("%d \t", i);
printf("\nDistance From Source : ");
for (int i = 0; i < V; ++i)
printf("%d \t",dist[i]);
return;
}
int main() {
int V = 5;
int E = 8;
struct Graph* graph = createGraph(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;
BellmanFord(graph, 0);
return 0;
}输出
Vertex : 0 1 2 3 4 Distance From Source : 0 -1 2 -2 1
更新于：2019年10月4日
4K+ 次浏览
广告