数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中的二项堆?
二项堆被定义为二叉堆的扩展，它提供了更快的合并或联合操作以及二叉堆提供的其他操作。
二项堆被视为二项树的集合。
什么是二项树？
k 阶二项树可以通过取两棵 k-1 阶二项树并将其中一棵作为另一棵的最左孩子来构建。
k 阶二项树具有以下属性。
二项树的节点数正好为 2k。
二项树的深度为 k。
在深度 i 处正好有 kCi 个节点，其中 i = 0, 1, . . . , k。
根节点的度数为 k，根节点的孩子本身被视为从左到右的 k-1、k-2、...0 阶二项树。
二项堆 -
二项堆被定义为一组二项树，其中每个二项树都遵循最小堆属性。并且对于任何度数，最多只能有一棵该度数的二项树。
二项堆示例 -
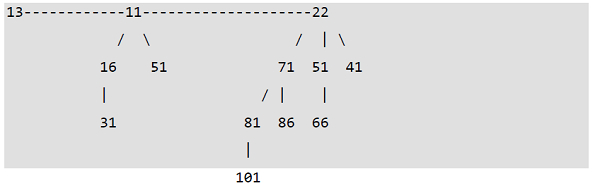
一个拥有 12 个节点的二项堆。它被视为 2 的集合
从左到右的 2 阶和 3 阶二项树
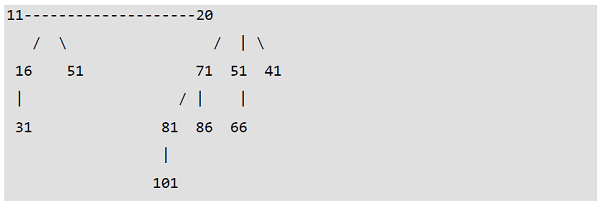
二项堆和数字的二进制表示
一个拥有 m 个节点的二项堆，其二项树的数量等于 m 的二进制表示中设置位的数量。例如，假设 m 为 13，m 的二进制表示（00001101）中有 3 个设置位，这表示 3 棵二项树。我们还可以将这些二项树的度数与设置位的位位置相关联。借助这种关系，我们可以确定或得出结论，在具有 'm' 个节点的二项堆中，有 O(logm) 棵二项树。
二项堆的操作 -
union() 是二项堆中的主要操作，所有其他操作主要实现此操作。union() 操作负责将两个二项堆合并成一个。
insert(h, K) - 将键 'K' 插入到二项堆 'h' 中。首先，此操作能够创建一个具有单个键 'K' 的二项堆，然后对 h 和新的二项堆调用 union。
getMin(h) - 获取最小值 getMin() 的一种简单方法是访问二项树根节点的列表并返回最小的键。
此应用程序需要 O(logm) 时间。可以通过维护指向最小键根节点的指针将其改进为 O(1)。
extractMin(h) - 此操作也实现了 union()。首先，我们调用 getMin() 来计算最小键二项树，接下来我们删除该节点并通过组合已删除最小节点的所有子树来创建一个新的二项堆。最后，我们对 h 以及新创建的二项堆调用 union()。此操作需要 O(logm) 时间。
delete(h) - 与二叉堆相同，首先，删除操作将键减少到负无穷大，接下来调用 extractMin()。
decreaseKey(h) - decreaseKey() 也与二叉堆相同。首先，我们将减小的键与其父节点进行比较，如果父节点的键更大，则交换键并对其父节点进行递归。最后，当我们到达父节点具有较小键的节点或到达根节点时停止。decreaseKey() 的时间复杂度为 O(logm)。
383 次查看
