数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中的 BK 树简介
BK 树或 Burkhard 树是一种数据结构形式，通常用于基于莱文斯坦距离执行拼写检查。它也用于字符串匹配，自动更正功能可以使用这种数据结构。假设我们在字典中有一些单词，我们需要检查其他一些单词是否存在拼写错误。我们需要有一个单词集合，这些单词接近于要检查拼写给定的单词。例如，如果我们有单词“uck”，正确的单词可以是（truck、duck、duck、suck）。因此，拼写错误可以通过删除一个单词或添加一个新单词来更正，用合适的字母替换一个字母。使用编辑距离作为参数并使用字典检查拼写。
与所有其他树一样，BK 树也由节点和边组成。节点表示字典中的单词。边包含一些整数权重，这些权重为我们提供从一个节点到另一个节点的编辑距离信息。
考虑一个包含单词 {book, books, boo, cake, cape} 的字典 -
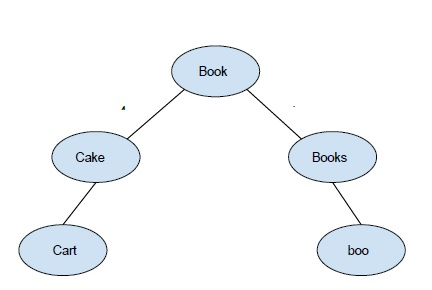
BK 树
BK 树中的每个节点都只有一个具有相同编辑距离的子节点。如果我们在插入节点时遇到一些编辑距离冲突，我们将传播插入过程，直到我们得到正确的子节点。每个插入都从根节点开始，根节点可以是任何单词。到目前为止，我们已经了解了什么是 Bk 树。现在让我们看看如何找到正确的最接近的单词。首先，我们需要设置容差值，此容差值只不过是我拼写错误的单词和正确单词之间的最大编辑距离。
为了在容差范围内找到合格的正确单词，我们使用迭代过程。但这具有较高的复杂度，因此现在 BK 树开始发挥作用，因为我们知道二叉树中的每个节点都是根据其与父节点的编辑距离构建的。因此，我们可以直接从根节点到位于容差范围内的特定节点。如果 TOL 是容差限制，并且当前节点与拼写错误的节点的编辑距离为 dist。所以现在，我们只迭代那些编辑距离在范围内的子节点。
[dist - TOL, dist+TOL]，这在很大程度上降低了复杂度。
示例
说明工作原理的程序 -
#include "bits/stdc++.h"
using namespace std;
#define MAXN 100
#define TOL 2
#define LEN 10
struct Node {
string word;
int next[2*LEN];
Node(string x):word(x){
for(int i=0; i<2*LEN; i++)
next[i] = 0;
}
Node() {}
};
Node RT;
Node tree[MAXN];
int ptr;
int min(int a, int b, int c) {
return min(a, min(b, c));
}
int editDistance(string& a,string& b) {
int m = a.length(), n = b.length();
int dp[m+1][n+1];
for (int i=0; i<=m; i++)
dp[i][0] = i;
for (int j=0; j<=n; j++)
dp[0][j] = j;
for (int i=1; i<=m; i++) {
for (int j=1; j<=n; j++) {
if (a[i-1] != b[j-1])
dp[i][j] = min( 1 + dp[i-1][j], 1 + dp[i][j-1], 1 + dp[i-1][j-1] );
else
dp[i][j] = dp[i-1][j-1];
}
}
return dp[m][n];
}
void insertValue(Node& root,Node& curr) {
if (root.word == "" ){
root = curr;
return;
}
int dist = editDistance(curr.word,root.word);
if (tree[root.next[dist]].word == ""){
ptr++;
tree[ptr] = curr;
root.next[dist] = ptr;
}
else{
insertValue(tree[root.next[dist]],curr);
}
}
vector <string> findCorrectSuggestions(Node& root,string& s){
vector <string> corrections;
if (root.word == "")
return corrections;
int dist = editDistance(root.word,s);
if (dist <= TOL) corrections.push_back(root.word);
int start = dist - TOL;
if (start < 0)
start = 1;
while (start < dist + TOL){
vector <string> temp = findCorrectSuggestions(tree[root.next[start]],s);
for (auto i : temp)
corrections.push_back(i);
start++;
}
return corrections;
}
int main(){
string dictionary[] = {"book","cake","cart","books", "boo" };
ptr = 0;
int size = sizeof(dictionary)/sizeof(string);
for(int i=0; i<size; i++){
Node tmp = Node(dictionary[i]);
insertValue(RT,tmp);
}
string word1 = "ok";
string word2 = "ke";
vector <string> match = findCorrectSuggestions(RT,word1);
cout<<"Correct words suggestions from dictionary for : "<<word1<<endl;
for (auto correctWords : match)
cout<<correctWords<<endl;
match = findCorrectSuggestions(RT,word2);
cout<<"Correct words suggestions from dictionary for : "<<word2<<endl;
for (auto correctWords : match)
cout<<correctWords<<endl;
return 0;
}输出
Correct words suggestions from dictionary for : ok book boo Correct words suggestions from dictionary for : ke cake
244 次浏览
