数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中的对称树
假设我们有一个二叉树，任务是检查它是否构成自身的镜像。对称二叉树构成其自身的镜像。
例如
输入-1
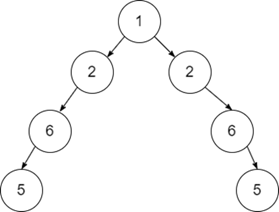
输出
True
解释
由于给定的二叉树构成其自身的镜像，因此输出为 True。
输入-2：
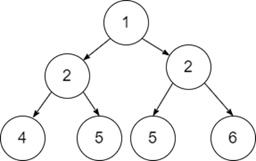
输出
False
解释
由于给定的二叉树没有构成其自身的镜像，因此它不是对称的。
解决此问题的方法
对称二叉树是一棵树，它是其自身的镜像，这意味着我们必须检查树的左右节点是否相同。
布尔函数将首先检查左节点和右节点。如果节点为空或为 NULL，则返回 True。对于其他情况，我们将检查它是否有左或右子节点，然后它们必须相同，以便它成为对称树。
- 取一个包含根及其子节点的二叉树。
- 布尔辅助函数 helper(node*root1, node*root2) 获取同一棵树的两个根，这有助于检查左子节点和右子节点是否相同。
- 如果树为空或为 NULL，则返回 True。
- 递归检查树的左节点和右节点是否相等。
- 如果不满足上述所有条件，则返回 False。
示例
#include<bits/stdc++.h>
using namespace std;
struct treenode {
int data;
treenode * left;
treenode * right;
};
struct treenode * createNode(int d) {
struct treenode * root = new treenode;
root -> data = d;
root -> left = NULL;
root -> right = NULL;
return root;
}
bool helper(struct treenode * root1, struct treenode * root2) {
if (root1 == NULL and root2 == NULL)
return true;
if (root1 and root2 and root1 -> data == root2 -> data)
return (helper(root1 -> left, root2 -> right) and helper(root1 -> right, root2 -> left));
return false;
}
bool isSymmetry(struct treenode * root) {
return helper(root, root);
}
int main() {
struct treenode * root = NULL;
root = createNode(4);
root -> left = createNode(2);
root -> right = createNode(2);
root -> left -> right = createNode(7);
root -> left -> left = createNode(5);
root -> right -> left = createNode(5);
root -> right -> right = createNode(7);
if (isSymmetry(root)) {
cout << "True" << endl;
} else {
cout << "False" << endl;
}
return 0;
}运行以上代码将生成以下输出：
输出
False
解释
由于给定的树不是对称的，因此我们得到输出 False。
更新于： 2021年2月23日
569 次查看
广告