检查矩阵A是否可以通过更改Python中任何子矩阵的角元素的奇偶性转换为B
假设我们有两个N X M二进制矩阵A和B。在单个操作中,我们可以选择一个子矩阵(至少2x2),并转换角元素的奇偶性(翻转位)。最后,我们必须检查是否可以通过执行任意数量的操作将矩阵A转换为B。
因此,如果输入如下所示:
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
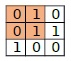
则输出为True,因为我们可以对mat1的左上角大小为(2x2)的子矩阵执行操作以获得mat2。
为了解决这个问题,我们将遵循以下步骤:
- row := mat1的行数
- column := mat1的列数
- 对于 i 从 1 到 row - 1:
- 对于 j 从 1 到 column - 1:
- 如果 mat1[i, j] 与 mat2[i, j] 不相同,则:
- mat1[i, j] := mat1[i, j] XOR 1
- mat1[0, 0] := mat1[0, 0] XOR 1
- mat1[0, j] := mat1[0, j] XOR 1
- mat1[i, 0] := mat1[i, 0] XOR 1
- 如果 mat1[i, j] 与 mat2[i, j] 不相同,则:
- 对于 j 从 1 到 column - 1:
- 对于 i 从 0 到 row - 1:
- 对于 j 从 0 到 column - 1:
- 如果 mat1[i, j] 与 mat2[i, j] 不相同,则:
- 返回 False
- 如果 mat1[i, j] 与 mat2[i, j] 不相同,则:
- 对于 j 从 0 到 column - 1:
- 返回 True
示例
让我们看下面的实现来更好地理解:
def solve(mat1, mat2): row = len(mat1) column = len(mat1[0]) for i in range(1, row): for j in range(1, column): if mat1[i][j] != mat2[i][j]: mat1[i][j] ^= 1 mat1[0][0] ^= 1 mat1[0][j] ^= 1 mat1[i][0] ^= 1 for i in range(row): for j in range(column): if mat1[i][j] != mat2[i][j]: return False return True mat1 = [ [1, 0, 0], [1, 0, 1], [1, 0, 0]] mat2 = [ [0, 1, 0], [0, 1, 1], [1, 0, 0]] print(solve(mat1, mat2))
输入
[ [1, 0, 0], [1, 0, 1], [1, 0, 0]], [ [0, 1, 0], [0, 1, 1], [1, 0, 0]]
输出
True

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP