检查数据集或特征的正态性

---

介绍

从统计学角度来看，正态性是指属于正态分布或高斯分布的现象。数据集的**正态性**是指检验数据集或变量是否遵循正态分布。可以进行许多检验来检查数据集的正态性，其中最流行的是直方图法、QQ图和KS检验。

正态性检验 – 检查正态性

确定数据集或特征的正态性既有统计方法，也有图形方法。让我们来看一下其中的一些方法。

图形方法

直方图

直方图以条形图的形式显示特征的分布。每个条形代表特定值的出现频率。它用于可视化单个特征。

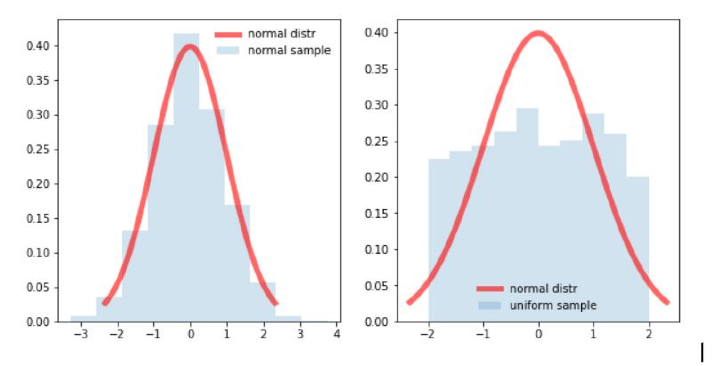
在上图中，我们可以看到左图比右图更接近钟形正态曲线。因此，我们可以推断左图是正态分布。

代码示例 [直方图]

import pandas as pd
df = pd.Series([11,12,13,14,15,16,17,18,8,3,5,7,9,23,30,34])
df.hist()

输出

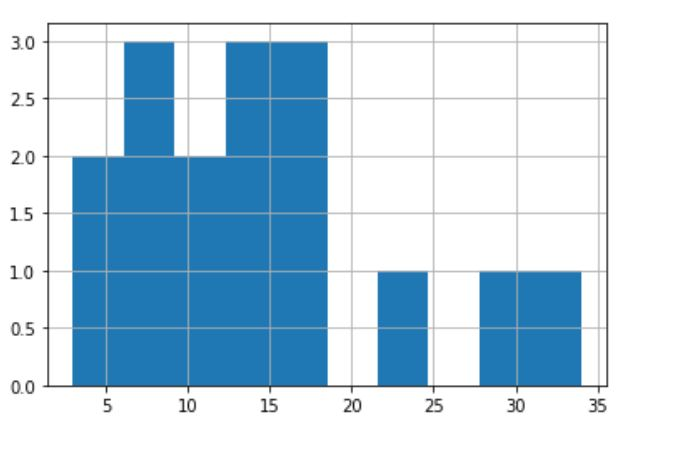
QQ图

也称为分位数-分位数图，它更清晰地显示了与正态分布的偏差，因为它将实际分位数与理论分位数作图。

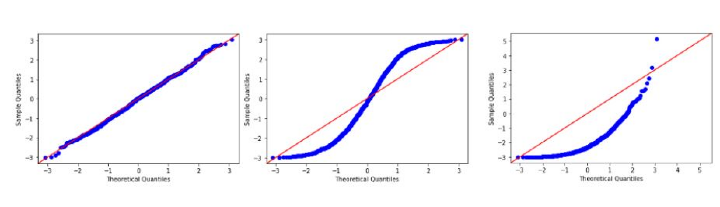
为了使数据或特征遵循正态分布，它应该更紧密地与上图中的红线对齐。在最左边的图像中，我们可以说它遵循正态分布，因为实际分位数与理论分位数一致。

代码示例 [QQ图]

import statsmodels.api as sapi
from scipy.stats import norm as nm
import matplotlib.pyplot as plt

data = nm.rvs(size=2000)
sapi.qqplot(data, line='45')
plt.show()

输出

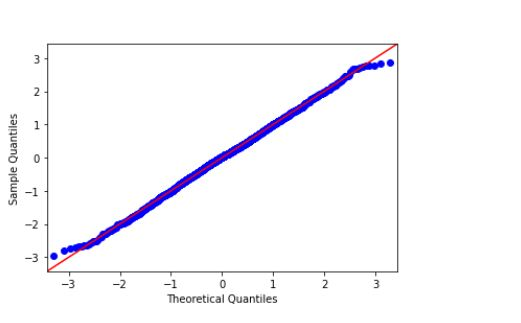
统计方法

KS检验

KS检验代表 Kolmogorov-Smirnov 检验。它通过测量经验分布和理论分布之间的距离来定义检验统计量。在KS检验中，Kolmogorov-Smirnov是检验统计量。我们寻找原假设为真，然后它遵循Kolmogorov分布。P值可以决定是否接受或拒绝原假设。为了使数据遵循正态分布，KS统计量的值应为0。

如果检验的P值大于0.05，我们得出结论：数据遵循正态分布；如果P值小于0.05，我们认为是非正态分布。

KS检验的缺点是它需要大量的数点才能拒绝原假设。异常值会影响KS检验。

代码示例 [KS检验]

from scipy.stats import norm,kstest
datapoints = norm.rvs(size=2000)
statks, pval = kstest(datapoints, 'norm')
print("statistics (KS) : ", statks,", pvalue : " ,pval)

输出

statistics (KS) :  0.021882913017164163 , pvalue :  0.2894024815418249

Shapiro-Wilk检验

这是一个非常强大的正态性检验。它也用于其他分布。

如果Wilk检验的P值大于0.05，我们得出结论：数据遵循正态分布；如果P值小于0.05，我们认为是非正态分布。

代码示例 [Wilk检验]

from scipy.stats import shapiro,norm
datapoints = norm.rvs(size=1000)
statistic_val,pval = shapiro(datapoints)
print("statistic : ", statistic_val,",  pvalue : " ,pval)

输出

statistic :  0.9993162155151367 , pvalue :  0.9813627600669861

结论

数据集或特征的正态性是数据分析中一个非常理想的特性。有很多很好的正态性检验，包括图形方法和统计方法。正态数据集在机器学习和数据科学中被认为是标准的，因为它包含有用的信息，并且大多数自然现象的数据都表现出正态性。