保守力和非保守力

---

简介

保守力和非保守力是物理学中对力的分类。对于做功与路径无关的力，认为是保守力。对于做功依赖于路径的力，则认为是非保守力。对于保守力，机械能的总和始终保持恒定，但对于非保守力，物体保持的机械能会减少一定量，并转化为其他形式，如热能、声能等。

什么是保守力？

保守力是指做功的大小仅由物体所经过的始末位置决定的力。如果闭合路径上的做功为零，则该力被称为保守力。任何系统的总能量（动能和势能之和）都是守恒的。重力、浮力和静电力都是保守力的例子。

什么是势能？

系统或物体由于其位置或构型而具有的能量称为势能。它是储存的或完全可恢复的能量。如果一个力所做的功不依赖于路径，则称该力为保守力。对于势能，所做的功仅取决于起始点和终点，而不取决于路径。因此，它是一种保守力。势能与非保守力无关。

哪些力是保守力？

对于做功仅取决于初始位置和最终位置，并且能量守恒的力，被认为是保守力。自然界中存在许多保守力，例如静电力、重力、浮力、弹簧恢复力等。

什么是非保守力？

非保守力是指做功依赖于物体运动轨迹的力。因此，在这种类型的力中，物体的起始位置和结束位置会影响所做的功。在此，机械能会转移到某些其他形式，在这些形式中无法进行功。因此，这种力也称为耗散力或降解力。粘度、电阻、空气阻力和摩擦力都是非保守力的例子。

• 空气阻力以波或湍流的形式降低或耗散能量。

• 摩擦力以热量和声能的形式降低能量。

保守力所做的功

如果所做的功与物体所经过的路径无关，则称为保守力。

请考虑下图：

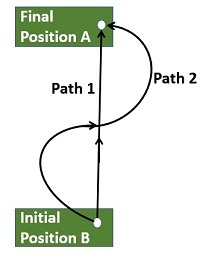
图1. 显示物体所经过路径的示意图

此处，路径 1 和路径 2 的做功相同。

做功

$$\mathrm{W=F×r}$$

其中 F 为力，r 为沿力方向移动的距离

假设 A 和 B 是路径的连接点，保守力所做的功表示为

$$\mathrm{W_{AB,path\:1}=\int F_{AB,path\:1} dr=W_{AB,path\:2}=\int F_{AB,path\:2} dr}$$

保守力和非保守力的区别

保守力和非保守力可以区分如下：

保守力	非保守力
做功与物体运动轨迹无关的力。	做功与物体运动轨迹相关的力。
如图 1 所示，在保守力中，路径 1 和路径 2 的做功相同。	如图 1 所示，在非保守力中，物体在路径 1 和路径 2 上所做的功不同。
在这种类型的力中，通过施加或去除外力，一种形式的能量完全转换为另一种形式。	在这种类型的力中，机械能会转移到某些其他形式，在这些形式中无法进行功。
总能量守恒。	由于耗散，能量会损失。
所做的功可以恢复。	所做的功无法恢复。
在闭合路径中，该力所做的功为零。	在路径中，该力所做的功不为零。
示例：重力、浮力、静电力	示例：粘度、电阻、空气阻力、摩擦力

表 1：保守力和非保守力的区别

保守力公式

保守力所做的功表示为

$$\mathrm{W=\int F.dx=-dU}$$

其中 F 为力，x 为距离的变化，U 为势能

然后我们可以写成：

$$\mathrm{F.dx=-dU}$$

重新排列后，我们得到保守力公式为

$$\mathrm{F=-\frac{dU}{dx}}$$

结论

在物理学中，力分为两类，即保守力和非保守力。做功与物体所经过的路径无关的力称为保守力。在此，通过施加或去除外力，一种形式的能量完全转换为另一种形式。非保守力是指做功依赖于物体运动轨迹的力。在此，机械能会转移到某些其他形式，在这些形式中无法进行功。

因此，这种力也称为耗散力或降解力。当物体沿与保守力相反的方向运动时，物体内部储存的能量称为势能。自然界中存在许多保守力，例如静电力、重力、浮力、弹簧恢复力等。保守力和非保守力的区分基于其性质。

常见问题

Q1. 如果力对物体做功，储存的能量会发生什么变化？

A1. 如果力对物体做功，则储存的能量会减少，反之亦然。储存的能量也称为势能。两个物体位置之间储存能量的差异是将物体从一个位置移动到另一个位置所需的功的总和。

Q2. 移动船只时的水阻力属于哪种类型的力？

A2. 移动船只时的水阻力是非保守力的一个例子。在非保守力中，所做的功依赖于物体的运动轨迹。

Q3. 往返行程中所做的功是多少？

A3. 闭合路径中所做的功为零。

Q4. 写出非保守力做功的表达式。

A4. 非保守力做功由以下公式给出：

$$\mathrm{ W=\Delta KE+\Delta PE }$$

其中 KE 为动能，PE 为势能

Q5. 弹性弹簧中的势能储备是多少？

A5. 弹性弹簧中的势能储备由以下公式给出：

$$\mathrm{PE=\frac{1}{2}kx^2}$$

其中 k 为弹簧常数，x 为长度变化。