数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++程序：计算圆柱体的体积和表面积
圆柱体是一种管状的3D物体，其底面为圆形，并具有一定的高度。圆柱体的体积实际上是它在空间中占据的空间大小。在本文中，我们将介绍几种用C++计算圆柱体体积和表面积的方法。
圆柱体有两个基本参数：高度h和底面半径r。圆柱体的表面积可以有两种变化：只有外曲面（对于空心且两端开口的圆柱体）和包含曲面以及两个平面（圆形）面的面积。
圆柱体的体积
要计算圆柱体的体积，我们需要两个输入：高度h和半径r。体积公式如下所示：
$$体积\:=\:\pi\:r^2*h$$
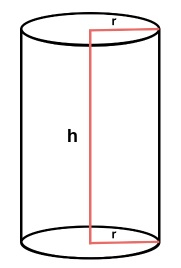
这里$\pi\:r^2$是底面积，用它乘以h将返回整个体积。现在让我们看看相应的算法和实现。
算法
- 读取输入的高度h和半径r
- 底面积 := $\pi\:r^2$
- 体积 := 底面积 * h
- 返回体积
示例
#include <iostream> using namespace std; float solve( float h, float r ) { float volume; float sa = 3.14159 * r * r; volume = sa * h; return volume; } int main() { cout << "Volume of a cylinder with height h = 5 cm, radius r = 2.5 cm, is " << solve( 5, 2.5 ) << " cm^3" << endl; cout << "Volume of a cylinder with height h = 25 in, radius r = 15 in, is " << solve( 25, 15 ) << " in^3" << endl; }
输出
Volume of a cylinder with height h = 5 cm, radius r = 2.5 cm, is 98.1747 cm^3 Volume of a cylinder with height h = 25 in, radius r = 15 in, is 17671.4 in^3
圆柱体的侧面积
如果我们将圆柱体展开成一个矩形薄片，其中宽度与h相同，长度与2𝜋𝑟（圆周长）相同，则可以计算出只有曲面的面积。在下图中，我们展示了如何将曲面展开成矩形。
$$侧面积\:=\:2\pi\:r*h$$
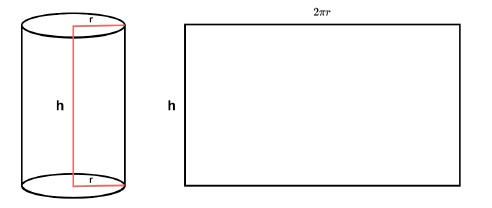
以下算法用于计算给定圆柱体的侧面积：
算法
- 读取输入的高度h和半径r
- 周长 := $2\pi\:r$
- 面积 := 周长 * h
- 返回面积
示例
#include <iostream> using namespace std; float solve( float h, float r ) { float area; float perimeter = 2 * 3.14159 * r; area = perimeter * h; return area; } int main() { cout << "Curved Surface Area of a cylinder with height h = 5 cm, radius r = 2.5 cm, is " << solve( 5, 2.5 ) << " cm^3" << endl; cout << "Curved Surface Area of a cylinder with height h = 25 in, radius r = 15 in, is " << solve( 25, 15 ) << " in^3" << endl; }
输出
Curved Surface Area of a cylinder with height h = 5 cm, radius r = 2.5 cm, is 78.5397 cm^3 Curved Surface Area of a cylinder with height h = 25 in, radius r = 15 in, is 2356.19 in^3
圆柱体的全面积
全面积由侧面积和圆柱体的两个圆形底面组成。因此，我们需要将它们与侧面积相加才能得到最终的面积。
$$侧面积\:=\:2\pi\:r*h$$
$$圆面积\:=\:\pi\:r\:^\:2$$
$$全面积\:=\:(侧面积)\:+\:2(圆面积)$$
由于有两个圆形平面，所以在相加之前我们将圆面积乘以2。这个想法在下图中进行了描述。与上图一样，矩形薄片也在那里，并且添加了两个圆形面。在下面的算法中，我们计算的是相同的。
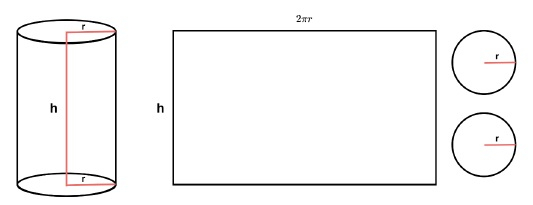
算法如下所示：
算法
- 读取输入的高度h和半径r
- 周长 := $2\pi\:r$
- 圆面积 :=$\pi\:r^2$
- 面积 := (周长 * h) + 2 * 圆面积
- 返回面积
示例
#include <iostream> using namespace std; float solve( float h, float r ) { float area; float perimeter = 2 * 3.14159 * r; float circle_area = 3.14159 * r * r; area = (perimeter * h) + (2 * circle_area); return area; } int main() { cout << "Complete Area of a cylinder with height h = 5 cm, radius r = 2.5 cm, is " << solve( 5, 2.5 ) << " cm^3" << endl; cout << "Complete Area of a cylinder with height h = 25 in, radius r = 15 in, is " << solve( 25, 15 ) << " in^3" << endl; }
输出
Complete Area of a cylinder with height h = 5 cm, radius r = 2.5 cm, is 117.81 cm^3 Complete Area of a cylinder with height h = 25 in, radius r = 15 in, is 3769.91 in^3
结论
要计算圆柱体的体积和面积，我们需要两个参数：圆柱体的底半径和高度。为了获得总的体积，首先需要计算底面积，然后将其乘以高度以获得实际体积。圆柱体的面积有两种形式：一种是侧面积，另一种是全面积，其中我们也考虑了底面的圆形平面。为了计算这一点，我们可以将圆柱体展开成一个高度为h，长度与圆周长相同的矩形薄片，那么这个矩形的面积就是侧面积。要获得全面积，我们需要将两个平面面积与侧面积相加。在上文的实现中，我们展示了使用一些示例输入来计算相同值的C++程序。对于每种情况，只需要两个输入h和r。
7K+ 浏览量
