数据处理与数据表示

---

介绍

数据处理和数据表示是系统地收集和呈现数据的过程。数据处理是指收集一组数据并将其以各种格式呈现的行为。收集、维护和呈现数据以促进分析、预测和决策的行为被称为数据处理。在本教程中，我们将简要讨论数据处理、集中趋势、频数表、如何在图表中表示数据以及与数据处理相关的示例。

什么是数据处理？

最初收集的观察结果称为原始数据。任何类型的数据都可以接受。可以包括文字、统计数据、测量值、描述或观察结果。数据管理是指确保在分析过程完成期间和之后安全可靠地收集、存储或处置研究数据的过程。

什么是集中趋势？

集中趋势的统计度量被定义为整个分布或数据集的单个值。它旨在对分布中的所有数据进行精确的描述。一般来说，可以使用几种统计度量来确定数据集的集中趋势。集中趋势有三种度量：

• 平均数 − 数据集的平均值由平均数表示。可以通过将数据集中的所有值的总和除以值的总数来确定。

• 中位数 − 数据集的中位数（无论它是按升序还是降序排列）是其中间值。当数据集中的项目数量为偶数时，可以通过对中间两个值取平均值来计算中位数。

• 众数 − 数据集中出现频率最高的值由众数表示。数据集有时可能有一个或多个众数，或者根本不包含任何众数。

什么是频数分布表？

在统计学中，频数分布表是对定量变量原始数据的排列的完整表示。该表显示变量的不同值的频数分布。频数分布有两种类型：离散型和连续型。可以使用计数标记为离散和连续数据值构建频数分布表。

数据的图形表示

数值数据的分析可以通过图形表示来完成。它使用图形来显示数据、想法、信息和概念之间的关系。特定区域中的信息类型始终是一个因素。线图、条形图、直方图、饼图和其他图形表示是各种类型的示例。

已解决示例

1) 求给定数据 23, 21, 18, 16, 15, 13, 12, 10, 9, 7, 6, 5, 2 的平均数。

答案 − 平均数 = 所有观测值的总和 / 观测值的总数 = (23 + 21 + 18 + 16 + 15 + 13 + 12 + 10 + 9 + 7 + 6 + 5 + 2) / 13 = 157 / 13 = 12.076

2) 求给定数据 34, 56, 5, 8, 19, 67, 23, 47, 11, 86 的中位数。

答案 − 总观测值是 10，为偶数，因此在按升序或降序排列后，我们需要计算中间两个数字的平均值。

按升序排列的数据是 5, 8, 11, 19, 23, 34, 47, 56, 67, 86。

中位数 = (23 + 34) / 2 = 28.5

3) 求给定数据 3, 5, 5, 8, 18, 6, 2, 7, 7, 8, 6, 7 的众数。

答案 − 众数是重复次数最多的数据，从以上数据中，5、6和8重复两次，7重复三次。因此，给定数据的众数是 7。

4) 为给定的 50 个值的数集构建类间距为 10 的频数分布。

111, 167, 124, 105, 138, 141, 154, 162, 125, 151, 122, 184, 171, 165, 158, 174, 156, 172, 160, 143, 132, 109, 113, 155, 162, 115, 116, 168, 105, 164, 154, 182, 147, 146, 198, 162, 160, 106, 193, 186, 191, 191, 112, 167, 178, 159, 158, 153, 144, 107

答案 − 给定类间距为 10，

100-110, 110-120，依此类推，直到 190-200

类间距	频数
100-110	5
110-120	4
120-130	3
130-140	2
140-150	5
150-160	10
160-170	11
170-180	4
180-190	3
190-200	3
总频数	50

5) 使用在示例 4 中构建的频数分布表计算给定数据集的平均数。

答案 − 要找到平均数，首先，我们需要找到类间距的中点，然后我们需要找到中点和频数的乘积。

类间距	频数 (f)	中点 (M)	f.M
100-110	5	105	525
110-120	4	115	460
120-130	3	125	375
130-140	2	135	270
140-150	5	145	725
150-160	10	155	1550
160-170	11	165	1815
170-180	4	175	700
180-190	3	185	555
190-200	3	195	585
总频数	50		总计 = 7560

现在平均数是 μ = Σ f.M / Σ f = 7560 / 50 = 151.2

6) 求以下数据的平均数

答案 − 要找到平均数，首先我们需要找到类间距的中点，然后我们需要找到中点和频数的乘积。

类间距	10-20	20-30	30-40	40-50	50-60	60-70	70-80	80-90	90-100
频数	4	6	8	10	12	14	7	5	6

类间距	频数 (f)	中点 (M)	f.M
10-20	4	15	60
20-30	6	25	125
30-40	8	35	280
40-50	10	45	450
50-60	12	55	660
60-70	14	65	550
70-80	7	75	525
80-90	5	85	425
90-100	6	95	570
总频数	72		总计 = 3645

现在平均数是 μ = Σ f.M / Σ f = 3645 / 72 = 50.625

7) 饼图被分成五个部分，每个部分的角度分别为 4x、7x、6x、3x 和 10x。确定 x 的度数值。

答案 − 饼图中所有角度的总和为 360°

4x + 7x + 6x + 3x + 10x = 360°

30x = 360° ⇒ x = 12°

8) 绘制以下给定年龄数据的直方图。

54,57,23,12,7,45,36,78,29,91,9,45,33,37,47,59,62,89,76,56,87,29,11,18,19,81,76, 75,56, 51,39,9,61,54,63

答案 −

现在可以使用频数直方图显示此数据。

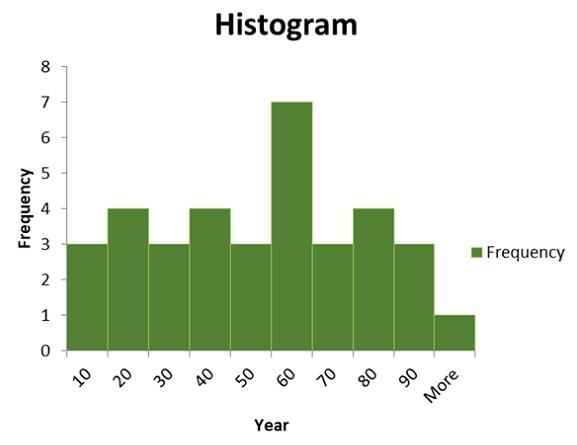
结论

数据管理是收集一组数据并将其以多种格式呈现的过程。“数据处理”是统计学中一个重要的概念，它确保研究数据的完整性，因为它处理多个关键方面，包括安全性、机密性和研究数据的保存。

常见问题

1. 与其他数据表示方法相比，图表有哪些优势？

使用图表的一些好处如下：

• 任何人都可以在没有任何预备知识的情况下理解图表。

• 它节省时间，使我们能够关联和对比来自不同时间段的事实。

• 它用于统计学，用于计算各种数据集的平均数、中位数和众数，以及用于数据插值和外推。

2. 数据处理涉及哪些步骤？

数据处理过程的步骤如下：

• 问题识别

• 数据收集

• 数据呈现

• 图形表示

• 数据分析

• 结论

3. 如何使用频数分布表？

频数分布表有助于对提供的数据进行计算。需要进行包括集中趋势、方差、统计检验和分析在内的计算。此外，频数分布表有助于以整洁且易于理解的方式呈现数据。

4. 存在哪些不同形式的频数分布？

以下是一些频数分布：

• 分组频数分布。

• 非分组频数分布。

• 累积频数分布。

• 相对频数分布。

• 相对累积频数分布