数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++表达式树的求值
在这个问题中，我们得到一个由诸如+，-，/，*之类的二元运算组成的表达式树。我们需要对表达式树进行求值，然后返回结果。
表达式树是一种特殊的二叉树，其中每个节点要么包含一个运算符，要么包含一个操作数，它们分布如下：
- 树的叶子节点是将要对其执行运算的值。
- 非叶子节点包含表示要执行的运算的二元运算符。
让我们举个例子来理解这个问题：
输入：
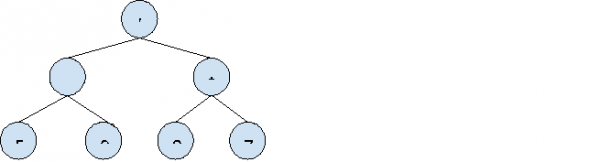
输出：1
解释：
解码表达式树：
表达式 = ( (5+9) / (2*7) )
= ( 14 / 14 )
= 1
解决方案
解决这个问题的一个简单方法是从根节点开始执行每个运算，对于操作数，我们将解决子树。由于所有运算都是二元的，因此树的节点要么有两个子节点，要么没有子节点。
我们将使用递归来解决每个节点的二元运算。
程序说明了我们解决方案的工作原理：
示例
#include <bits/stdc++.h>
using namespace std;
class node {
public:
string value;
node *left = NULL, *right = NULL;
node(string x)
{
value = x;
}
};
int solveExpressionTree(node* root) {
if (!root)
return 0;
if (!root->left && !root->right)
return stoi(root->value);
int leftSubTreeSol = solveExpressionTree(root->left);
int rightSubTreeSol = solveExpressionTree(root->right);
if (root->value == "+")
return leftSubTreeSol + rightSubTreeSol;
if (root->value == "-")
return leftSubTreeSol - rightSubTreeSol;
if (root->value == "*")
return leftSubTreeSol * rightSubTreeSol;
if (root -> value == "/")
return leftSubTreeSol / rightSubTreeSol;
return -1;
}
int main()
{
node *root = new node("/");
root->left = new node("+");
root->left->left = new node("9");
root->left->right = new node("5");
root->right = new node("*");
root->right->left = new node("2");
root->right->right = new node("7");
cout<<"The evaluation of expression tree is "<<solveExpressionTree(root);
return 0;
}输出：
The evaluation of expression tree is 1
更新于：2021年1月22日
968 次浏览
广告