数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究Python 程序构建给定表达式的表达式树
表达式树是指叶子节点包含要操作的值，而内部节点包含对叶子节点执行的操作符的树。
例如：4 + ((7 + 9) * 2) 将具有如下所示的表达式树 -
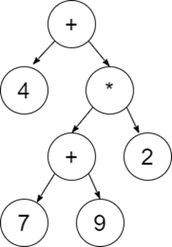
解决此问题的方法
为了为给定表达式构建表达式树，我们通常使用栈数据结构。最初，我们遍历给定的后缀表达式并遵循以下步骤 -
- 如果我们在给定表达式中得到一个操作数，则将其压入栈中。它将成为表达式树的根。
- 如果一个操作符在表达式中得到两个值，则将其作为子节点添加到表达式树中，并将它们压入当前节点。
- 重复步骤 1 和步骤 2，直到我们完成给定表达式。
示例
class stack: def __init__(self): self.arr = [] def push(self, data): self.arr.append(data) def pop(self): try: return self.arr.pop(-1) except: pass def top(self): try: return self.arr[-1] except: pass def size(self): return len(self.arr) # node class for expression tree class node: def __init__(self, data): self.data = data self.left = None self.right = None # expression tree class class exp_tree: def __init__(self, postfix_exp): self.exp = postfix_exp self.root = None self.createTree(self.exp) def isOperator(self, char): optr = [" ", "-", "*", "/", "^"] if char in optr: # if given char is operator return True # then return true return False # else return false def createTree(self, exp): s = stack() # store those operator node whose any child node is NULL self.root = node(exp[-1]) # last character of postfix expression is always an operator s.push(self.root) # travel on rest of the postfix expression for i in "".join(reversed(exp[:-1])): curr_node = s.top() if not curr_node.right: # if right node of current node is NULL temp = node(i) curr_node.right = temp if self.isOperator(i): s.push(temp) else: # if left node of current node is NULL temp = node(i) curr_node.left = temp # if no child node of current node is NULL s.pop() # pop current from stack if self.isOperator(i): s.push(temp) def inorder(self, head): # inorder traversal of expression tree # inorder traversal = > left, root, right if head.left: self.inorder(head.left) print(head.data, end=" ") if head.right: self.inorder(head.right) def infixExp(self): # inorder traversal of expression tree give infix expression self.inorder(self.root) print() if __name__ == "__main__": postfixExp = "ab ef*g*-" et = exp_tree(postfixExp) et.infixExp()
运行以上代码将生成如下输出：
输出
(a + b - e * f * g)
解释
从给定表达式构建树将生成这样的输出：操作数将成为节点的根，其余数字将成为表达式树的子节点。
更新于： 2021 年 2 月 23 日
2K+ 浏览量
广告