数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会研究
时尚研究
法律研究乘法两数的最快方法
两个数字以二进制字符串的形式给出，我们的任务是以一种更快、更有效的方式求出这些数字的乘积结果。
使用分而治之策略，我们可以非常有效地解决这个问题。我们将数字分成两部分。
设 Xleft 和 Xright 是第一个数字 X 的两个部分，Yleft 和 Yright 是第二个数字 Y 的两个部分。所以乘积为；
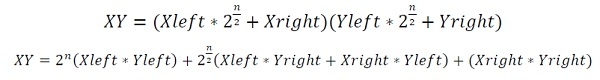
为了简单些，我们可以执行此操作
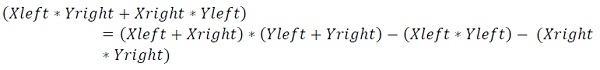
输入和输出
Input: Two binary numbers: 1101 and 0111 Output: The result is: 91
算法
addBitString(num1, num2)
输入：两个要相加的数字。
输出：相加后的结果。
Begin adjust num1 and num2 lengths length := length of num1 carry := 0 for i := length -1 down to 0, do num1Bit := num1[i] num2Bit := num2[i] sum := num1Bit XOR num2Bit XOR carry finalSum := sum + finalSum carry := (num1Bit AND num2Bit) OR (num2Bit AND carry) OR (num1Bit AND carry) done if carry ≠ 0, then finalSum := 1 + finalSum return finalSum End
multiply(num1, num2)
输入：两个要相乘的数字。
输出：相乘后的结果。
Begin adjust num1 and num2 lengths length := length of num1 if n = 0, then return 0 if n = 1, then return (num1[0] * num2[0]) firstHalf := n/2 secondHalf := (n - firstHalf) n1Left := substring of (0 to firstHalf) from num1 n1Right := substring of (firstHalf to secondHalf) from num1 n2Left := substring of (0 to firstHalf) from num2 n2Right := substring of (firstHalf to secondHalf) from num2 p1 := multiply(n1Left, n2Left) p2 := multiply(n1Right, n2Right) add1 := addBitString(n1Left, n1Right) add2 := addBitString(n2Left, n2Right) p3 := multiply(add1, add2) mask1 := shift 1 to left for 2*secondHalf bits mask2 := shift 1 to left for secondHalf bits return P1*mask2 + (p3 – p1 – p2)*mask2 + p2 End
示例
#include<iostream>
using namespace std;
int lengthAdjust(string &num1, string &num2) { //adjust length of binary string and send length of string
int len1 = num1.size();
int len2 = num2.size();
if (len1 < len2) {
for (int i = 0 ; i < len2 - len1 ; i++)
num1 = '0' + num1; //add 0 before the first string
} else if (len1 > len2) {
for (int i = 0 ; i < len1 - len2 ; i++)
num2 = '0' + num2; //add 0 before the second string
}
return num1.size();
}
string addBitStrings(string num1, string num2) {
string finalSum;
int length = lengthAdjust(num1, num2); //adjust and update number lengths and store length
int carry = 0; // Initialize carry
for (int i = length-1 ; i >= 0 ; i--) {
int num1Bit = num1[i] - '0';
int num2Bit = num2[i] - '0';
int sum = (num1Bit ^ num2Bit ^ carry)+'0'; //we know sum = A XOR B XOR C
finalSum = (char)sum + finalSum;
//the carry = (A AND B) OR (B AND C) OR (C AND A)
carry = (num1Bit&num2Bit) | (num2Bit&carry) | (num1Bit&carry);
}
if (carry) //when carry is present
finalSum = '1' + finalSum; //add carry as MSb
return finalSum;
}
long int multiply(string num1, string num2) {
int n = lengthAdjust(num1, num2); //find length after adjusting them
if (n == 0) //when there is 0 length string, return 0
return 0;
if (n == 1)
return (num1[0] - '0')*(num2[0] - '0'); //perform single bit muliplication
int firstHalf = n/2; // First half range
int secondHalf = (n-firstHalf); // Second half range
string num1Left = num1.substr(0, firstHalf); //first half of number 1
string num1Right = num1.substr(firstHalf, secondHalf); //second half of number 1
string num2Left = num2.substr(0, firstHalf);
string num2Right = num2.substr(firstHalf, secondHalf);
// find left right multiplication, and multiply after adding left and right part
long int P1 = multiply(num1Left, num2Left);
long int P2 = multiply(num1Right, num2Right);
long int P3 = multiply(addBitStrings(num1Left, num1Right), addBitStrings(num2Left, num2Right));
return P1*(1<<(2*secondHalf)) + (P3 - P1 - P2)*(1<<secondHalf) + P2;
}
int main() {
string num1, num2;
cout << "Enter First number in Binary: "; cin >>num1;
cout << "Enter Second number in Binary: "; cin >>num2;
cout << "The result is: " << multiply(num1, num2);
}输出
Enter First number in Binary: 1101 Enter Second number in Binary: 0111 The result is: 91
更新于： 17-Jun-2020
561 次浏览
广告