同态

如果给定两个图 G₁ 和 G₂可以通过从图 'G' 切割一些边和一些顶点来获得，则称这些图是同构的。请看下面的示例 -

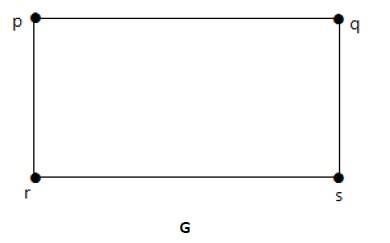
将边 'rs' 切割成两条边，方法是添加一个顶点。

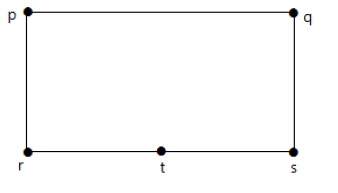
下面显示的图同构于第一个图。

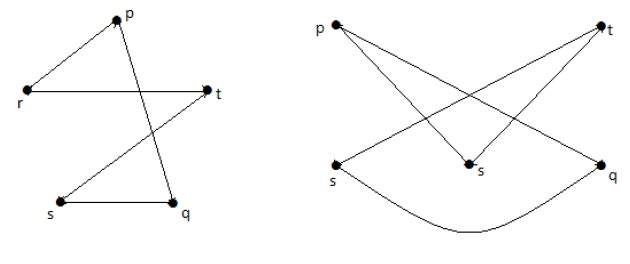
如果 G₁ 同构于 G₂，则 G 同构于 G₂，但反之不一定成立。

• 具有 4 个或更少顶点的任何图都是平面的。

• 具有 8 条或更少边的任何图都是平面的。

• 完全图 K_n 仅在 n ≤ 4 时是平面的。

• 完全二分图 K_{m, n} 仅在 m ≤ 2 或 n ≤ 2 时是平面的。

• 具有最小顶点数的简单非平面图是完全图K₅。

• 具有最小边数的简单非平面图是 K_{3, 3}。

多面体图

一个简单的连通平面图称为多面体图，如果该图中每个顶点的度数≥ 3，即 deg(V) ≥ 3 ∀ V ∊ G。

• 3|V| ≤ 2|E|
• 3|R| ≤ 2|E|

Mahesh Parahar 翻译

更新于： 2019-08-23

1 千次浏览

开启您的 职业生涯

完成课程并获得认证

开始学习