Seaborn 箱线图中如何确定异常值？

---

什么是异常值？

异常值是指数据集中的数据点或观测值，它们远离其他点。异常值可能是由测量误差、数据输入误差或实验误差等原因造成的。异常值会歪曲数据集，从而影响统计分析，并可能增加数据集的标准差，进一步影响模型预测。

异常值可能是有效的数据点，也可能是噪声。

为了更好地理解，让我们来看一个示例场景。假设您正在收集学生身高数据（年龄在 9 到 12 岁之间）。大多数学生身高都在 4 英尺左右。但有一些学生输入了错误的身高，例如 7 英尺。这个不寻常且不正确的数值就是异常值，因为它与其他数值有显著差异。简单来说，异常值就像“异类”，与组中其他成员不太相符。

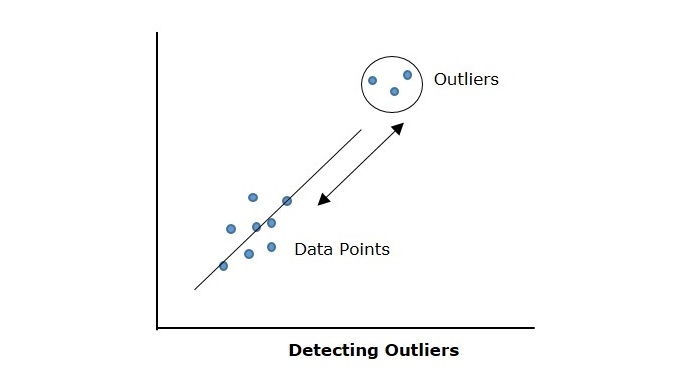
为什么要移除异常值？

移除异常值是数据预处理的重要步骤。如果数据集包含异常值，如果不移除并在该数据集上训练机器学习模型，则模型也会尝试覆盖异常值点，这会导致预测模型的泛化能力差。

在这种情况下，在覆盖异常值时，模型变得复杂，从而导致过拟合并在新数据集上产生错误预测。移除异常值最简单的方法之一是使用箱线图，以下部分讨论了如何借助箱线图识别异常值。

箱线图的统计分析

箱线图也称为盒须图，它是数据集分布的图形表示。它可以帮助我们解释数据点是分散还是集中。它还解释了数据集的偏度。

使用箱线图，我们可以了解数据集的最小值、最大值和四分位数范围（Q1、Q2、Q3）的统计信息。

其中 -

• 最小值 - 最小值确定数据集中的最小数据点。

• 最大值 - 最大值确定数据集中的最大数据点。

• 第一四分位数 (Q1) - 当数据点分成两半时，Q1 是数据点下半部分的中位数。它是数据点的第 25 个百分位数。

• 第二四分位数或中位数 (Q2) - Q2 是所有数据点的中位数。

• 第三四分位数 (Q3) - 当数据点分成两半时，Q3 是数据点上半部分的中位数。它是数据点的第 75 个百分位数。

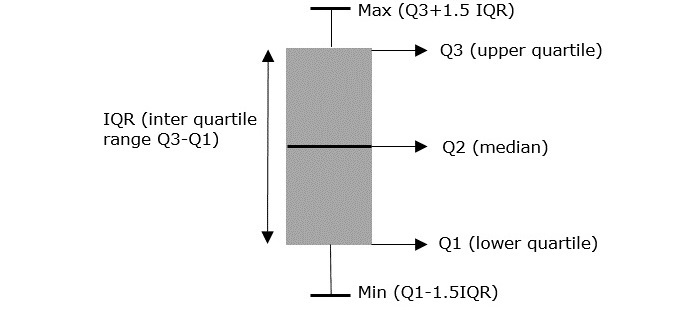
在任何数据集中，大于 Q3+1.5IQR 或小于 Q1-1.5IQR 的记录都被认为是异常值。

盒子越长，数据越分散，盒子越短，数据越集中。

使用 Seaborn 检测异常值

Seaborn 是一个基于 matplotlib 的数据可视化库，它可以创建复杂的可视化绘图，并提供默认调色板，从而生成美观的绘图。

我们可以使用 Seaborn 中的 boxplot() 函数创建箱线图。以下是 Seaborn 中 boxplot() 函数的语法：

seaborn.boxplot(x=, y=, heu=, data=)

其中，

• x、y、hue - 数据集中特征的名称。

• data - 用于绘图的数据集。

示例

在以下示例中，我们将使用箱线图绘制泰坦尼克号数据集，并尝试确定其中的异常值。

在这个泰坦尼克号数据集中，我们有 891 条记录和 15 个特征，描述了泰坦尼克号上乘客的生存状况。

以下是数据集中的前五行。

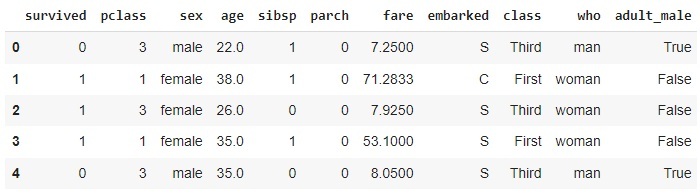
当我们使用“sns.boxplot()”为“age”特征绘制箱线图时，高于最大值和低于最小值的数据点被认为是异常值。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

dataset= sns.load_dataset('titanic')
sns.boxplot(y=dataset['age'])
plt.show()

输出

执行上述程序后，您将获得以下输出：

考虑到输出，可以看出，Age>65 是异常值点。

示例

由于我们在上述示例中使用了单个数值特征，因此我们在此考虑了 x 轴上的一个分类特征（alive）和 y 轴上的一个数值特征（age）。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

dataset= sns.load_dataset('titanic')
sns.boxplot(data=dataset, x="alive", y="age")
plt.show()

输出

执行上述程序后，您将获得以下输出：

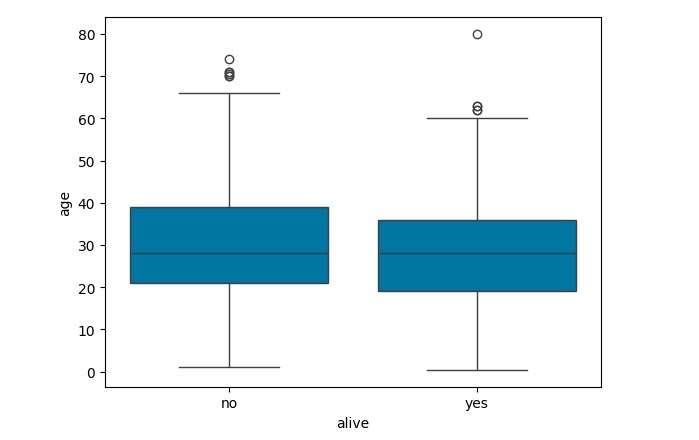
示例

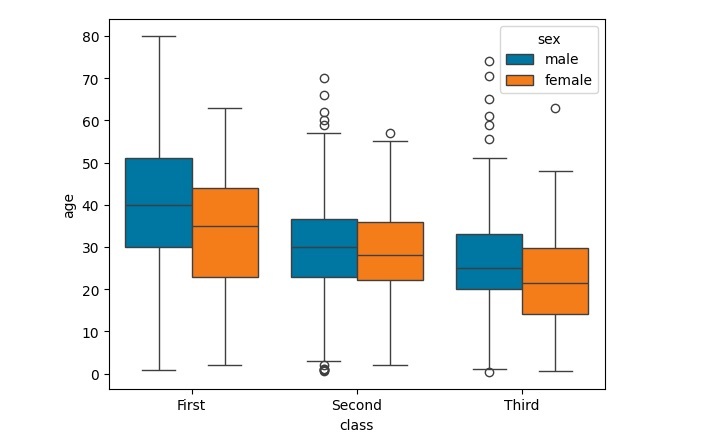
在这里，我们考虑了一个分类特征（class）并确定了相对于年龄特征的异常值，将图与另一个分类特征（sex）进行比较。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

dataset= sns.load_dataset('titanic')
sns.boxplot(x="class",y="age",hue="sex",data=dataset)
plt.show()

输出

执行上述程序后，您将获得以下输出：

删除异常值

删除异常值的一种方法是识别最小值和最大值，并丢弃超出此范围的数据点（将其设为空值并删除它们）。

示例

在以下示例中，我们选择年龄特征并移除识别的异常值：

• 我们首先必须计算 Q1 和 Q3 值，然后计算四分位数范围 (Q3-Q1)。

• 计算完四分位数范围后，计算 Q3+1.5IQR 和 Q1-1.5IQR 的值，如指定的那样，如果数据点大于 Q3+1.5IQR 且小于 Q1-1.5IQR，则认为这些数据点是异常值。

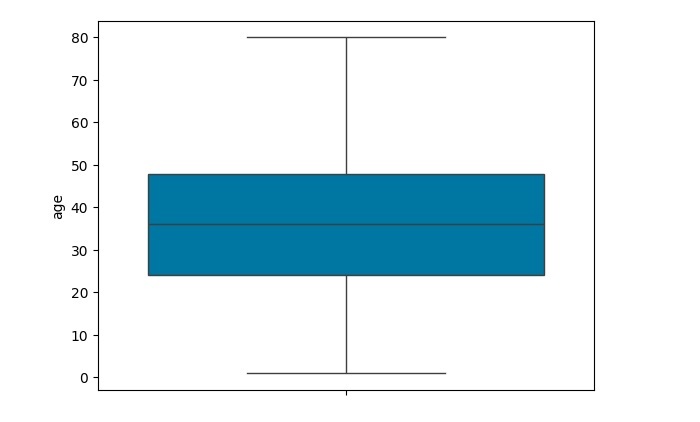
• 最后，将这些异常值替换为空值，然后使用 .dropna 删除这些空值。再次绘制箱线图检查是否已移除异常值。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

dataset= sns.load_dataset('titanic')
for i in ['age']:
   q75,q25=np.percentile(dataset.loc[:,i],[75,25])
   intr_qr= q75-q25
   max = q75+(1.5*intr_qr)
   min = q25-(1.5*intr_qr)
   dataset.loc[dataset[i]<min,i]=np.nan
   dataset.loc[dataset[i]>max,i]=np.nan  
dataset=dataset.dropna(axis=0)
sns.boxplot(y=dataset['age'])
plt.show()

输出

执行上述程序后，您将获得以下输出：