数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学使用Python讲解金融概念
Python 提供了各种工具和库，帮助我们处理概率的基础知识。概率在各个领域都有广泛的应用，从 AI 内容检测到纸牌游戏。random 模块常用于概率相关的题目。结合 numpy 和 scipy 等库（以及 matplotlib 和 seaborn 用于可视化），当数据规模很大且主要以 csv 文件形式存在时，这将非常有用。概率问题可以进一步与统计学结合起来，以获得更多见解。无论您是初学者还是实践者，在概率领域总有更多知识需要学习。
Python 可用于辅助这些金融概念，从而减少所需的人工输入并简化流程。一些可以使用 Python 实现的关键金融概念如下：
TVM − 货币时间价值论述了由于通货膨胀和利率等因素，资金的价值会随时间而变化。
利息计算 − 可以借助 Python 计算各种利息，例如单利、复利和连续复利。
投资组合优化 − 这是选择各种投资并预测最大化收益和最小化风险的方法的过程。
蒙特卡洛模拟 − 这是一种统计技术，可用于模拟和分析一段时间内金融系统的行为。
算法交易 − 自动化交易算法，可根据市场状况和各种相关因素做出买卖决策。
TVM
TVM 代表货币时间价值，这是一个金融概念，根据该概念，现在的一笔钱由于其在期间内的盈利潜力，在未来将价值较低。这就好比说，1958 年的 100 卢比与今天的 8411 卢比具有相同的价值。TVM 受通货膨胀、风险、市场状况等多种因素的影响。
TVM 公式为：
$$\mathrm{FV = PV * (1 + r)^{n}} $$
其中：
FV 代表未来值，
PV 代表现值，
r 代表利率，
n 代表投资持有期间（例如年数）。
这是一个使用 Python 演示 TVM 的简单程序。
示例
def tvm(pv, r, n):
fv = pv * (1 + r) ** n
return fv
pv = 10000
r = 0.05
n = 10
fv = tvm(pv, r, n)
print("Future Value of ₹",pv,"in",n,"years will be ₹", fv)
输出
Future Value of ₹ 10000 in 10 years will be ₹ 16288.94626777442
利息计算
利息是借钱需支付的额外费用，或者是你借出钱收取的费用。利息分为不同类型：
单利：利息仅支付初始本金。
示例
def simple_interest(principal, rate, time):
interest = principal * rate * time
return interest
principal = 10000.0
rate = 0.05
time = 2
# simple interest is principal * time * rate / 100
interest = simple_interest(principal, rate, time)
print("Simple Interest on Rs",principal,"will amount to Rs", interest)
输出
Simple Interest on Rs 10000.0 will amount to Rs 1000.0
复利：利息支付基于初始本金和到期日的利息。
示例
def compound_interest(principal, roi, time_period):
interest_paid = principal_amt * (pow((1 + roi / 100), time_period))
return interest_paid-principal_amt
principal = 10000
rate = 5
time = 2
interest = compound_interest(principal, rate, time)
print("Compound interest on Rs",principal,"will amount to Rs", round(interest,2))
输出
Compound interest on Rs 10000 will amount to Rs 1025.0
投资组合优化
在这里，我们选择资产组合以最大限度地降低风险并最大限度地提高收益或回报。这被称为优化，在金融领域非常有用。现代投资组合理论是一个非常有用的数学模型。
示例
import numpy as np import cvxpy as cp # Define the expected return and covariance matrix returns = np.array([0.1, 0.2, 0.15]) covariance = np.array([[0.015, 0.01, 0.005], [0.01, 0.05, 0.03], [0.005, 0.03, 0.04]]) # Define the optimization problem weights = cp.Variable(len(returns)) risk = cp.quad_form(weights, covariance) returns = returns @ weights obj = cp.Minimize(risk) constraints = [sum(weights) == 1, weights >= 0] prob = cp.Problem(obj, constraints) # Solve the optimization problem prob.solve() # Print the optimized weights print(weights.value)
输出
[7.77777778e-01 4.49548445e-23 2.22222222e-01]
在上面的示例中，定义了三种资产的预期收益和协方差矩阵。然后定义了一个投资组合优化问题，并在此处使用了 Python 的 cvxpy 库，该库在权重之和等于 1 以及权重非负的约束条件下最小化投资组合风险。
此优化问题的解决方案预测了投资组合中每种资产的最佳权重。
蒙特卡洛模拟
蒙特卡洛模拟是一种模拟方法，通常用于通过使用概率分布进行随机抽样来模拟系统的行为。它可以通过重复迭代和平均结果来预测复杂系统的结果。
示例
import numpy as np
import matplotlib.pyplot as plt
# Define the parameters
mean = 0.1
stddev = 0.2
num_simulations = 1000
num_steps = 20
# Generate the simulated returns
returns = np.random.normal(mean, stddev, (num_simulations, num_steps))
# Calculate the cumulative returns
cumulative_returns = (returns + 1).cumprod(axis=1)
# Plot the results
plt.plot(cumulative_returns.T)
plt.xlabel("Time Step")
plt.ylabel("Cumulative Return")
plt.title("Monte Carlo Simulation of Stock Returns")
plt.show()
输出
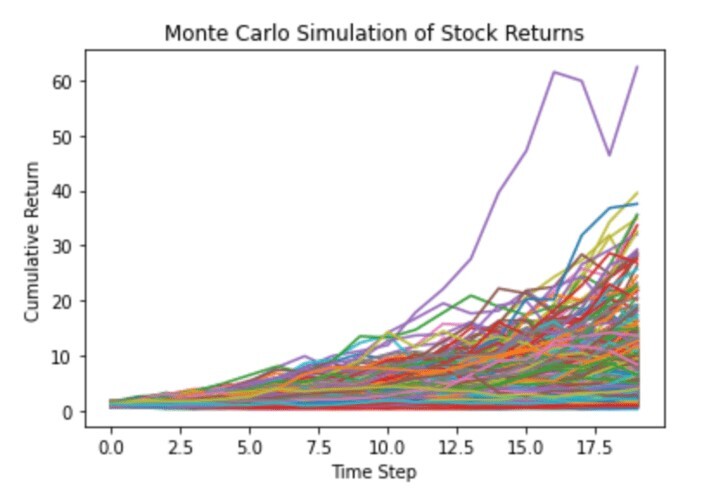
算法交易
利用数学和统计分析识别并帮助系统地执行交易，从而自动化金融市场中资产的买卖过程。其主要目标是根据某些固定规则和数据而不是主观判断（可能导致歧义）来执行交易。
下面使用的 (stock_data.csv) 数据集链接在此处。
示例
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Load the stock data
df = pd.read_csv("stock_data.csv")
df["Date"] = pd.to_datetime(df["Date"])
df.set_index("Date", inplace=True)
# Run algorithmic trading strategy
capital = 1000
shares = 0
for i in range(1, len(df)):
if df.iloc[i]["Close"] > df.iloc[i-1]["Close"]:
# Buy shares
shares += capital // df.iloc[i]["Close"]
capital -= shares * df.iloc[i]["Close"]
elif df.iloc[i]["Close"] < df.iloc[i-1]["Close"]:
# Sell shares
capital += shares * df.iloc[i]["Close"]
shares = 0
# Plot the results
df["Close"].plot()
plt.title("Stock Price")
plt.xlabel("Date")
plt.ylabel("Close Price")
plt.show()
# Output the final capital
print("Final capital: ${:.2f}".format(capital + shares * df.iloc[-1]["Close"]))
输出
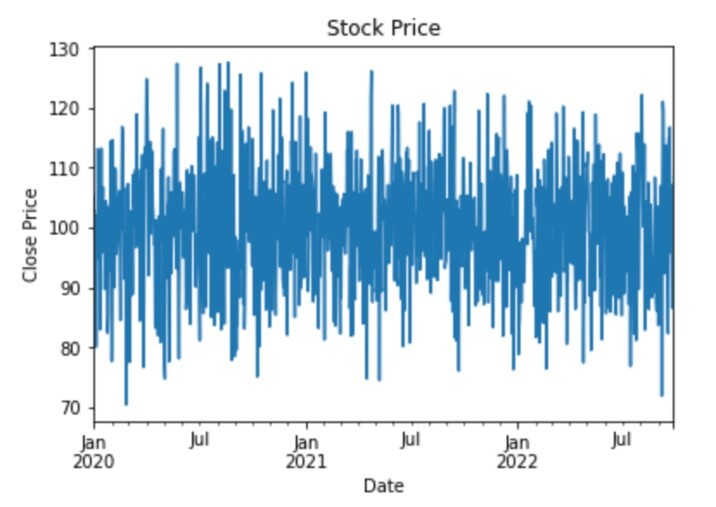
Final capital: $34.25
结论
使用 Python，可以实现大量的金融概念，从算法交易到货币时间价值。Numpy、pandas、matplotlib 等库提供了各种工具，可帮助进行数据处理、分析和可视化，以进行财务分析。Python 的易用性和可读性使其不仅对专业人士，而且对学生都非常有用。虽然我们的目标是实现最大精度并做出最佳决策，但错误仍然可能发生，并可能导致巨大损失，因此在将其应用于现实生活之前，了解风险非常重要。
119 次浏览
