C 中帕斯卡三角的打印

帕斯卡三角是教授工程学的学生时的经典示例之一。它有很多种解释。其中一种著名的解释就是使用二项式方程。

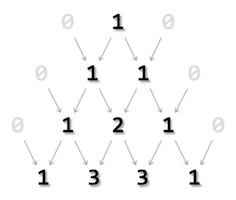
三角形外的所有值都视为零 (0)。第一行为 0 1 0，而只有 1 出现在帕斯卡三角中，0 是不可见的。第二行是通过添加 (0+1) 和 (1+0) 获得的。输出被夹在两个零之间。该过程将一直持续到达到所需级别。

可以通过二项式定理推导出帕斯卡三角形。我们可以使用组合和阶乘来实现这一点。

算法

假设我们很清楚阶乘，我们以分步方式研究绘制帕斯卡三角形的基本概念 −

START
  Step  1 - Take number of rows to be printed, n.
  Step  2 - Make outer iteration I for n times to print rows
  Step  3 - Make inner iteration for J to (N - 1)
  Step  4 - Print single blank space " "
  Step  5 - Close inner loop
  Step  6 - Make inner iteration for J to I
  Step  7 - Print nCr of I and J
  Step  8 - Close inner loop
  Step  9 - Print NEWLINE character after each inner iteration
  Step 10 - Return
STOP

伪代码

我们可以针对以上算法推导出如下伪代码 −

procedure pascals_triangle

   FOR I = 0 to N DO
      FOR J = 0 to N-1 DO
         PRINT " "
      END FOR

      FOR J = 0 to I DO
         PRINT nCr(i,j)
      END FOR

      PRINT NEWLINE
   END FOR

end procedure

实现

让我们实现此程序的全部内容。我们实现阶乘函数 (非递归) 和 ncr (组合)。

#include <stdio.h>

int factorial(int n) {
   int f;
   
   for(f = 1; n > 1; n--)
      f *= n;
      
   return f;
}

int ncr(int n,int r) {
   return factorial(n) / ( factorial(n-r) * factorial(r) );
}

int main() {
   int n, i, j;

   n = 5;

   for(i = 0; i <= n; i++) {
      for(j = 0; j <= n-i; j++)
         printf("  ");
         
      for(j = 0; j <= i; j++)
         printf(" %3d", ncr(i, j));

      printf("\n");
   }
   return 0;
}

输出应如下所示 −

               1
             1   1
           1   2   1
         1   3   3   1
       1   4   6   4   1
     1   5  10  10   5   1