反射镜方程

---

引言

光是一种电磁辐射，是电磁波谱中唯一可见于人眼的部分。如果光照亮任何表面，则表面接收到的光量取决于光源与表面的距离。当光线照射到粗糙表面时，它会在各个方向上散射。但是对于抛光表面，由于光的反射，会在特定角度看到适当的照明。为了理解反射镜成像的原因以及为什么它们不会产生相同类型的图像，使用了反射镜方程的概念。

什么是镜子？

能够反射放置在其前的物体图像的表面称为镜子。

• 镜子成像的现象取决于反射定律。当来自物体的光线照射到镜子上时，会以一定的角度反射，从而形成图像。

• 镜子表面光滑，因此会发生镜面反射，光线在一个方向上反射有助于它们成像，但任何其他白色平面表面都具有粗糙的表面，使其发生漫反射，光线在各个方向上反射，因此无法形成图像。

• 镜子具有平面或曲面。镜子有三种类型：平面镜、凹面镜和凸面镜。

凹面镜

它是球面镜的一部分，从外表面涂漆，并将光线从内表面反射到其中一个内焦点。

• 它是一个会聚镜，因为它会聚集照射在其上的光线，并将所有平行光线聚焦到镜子的焦点。

• 这种镜子与凸面镜不同，因为它可以形成大小不同的实像或虚像，这都取决于镜子和物体之间的距离。

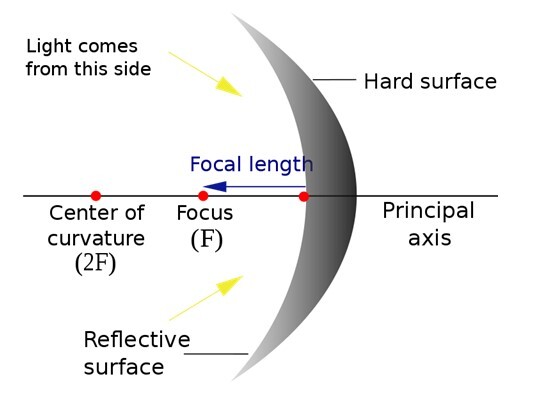
图1：凹面镜示意图 I, Cronholm144, 凹面镜, CC BY-SA 3.0

凸面镜

它也是一个空心球面镜的一部分，其反射面位于镜子的凸出侧，从其曲面涂漆，并将光线从外表面向外反射，因此不能用来聚焦光线。

• 它是一个发散镜，仅形成虚像，永远无法投射到屏幕上，因为该镜子的焦点和曲率中心位于镜子内部，并且如以下图表所示，是无法达到的。

• 这些镜子总是只能形成较小的虚像（缩小的像），但是如果物体靠近镜子，图像会变大（放大）。

图2：凸面镜 I, Cronholm144, 凸面镜1, CC BY-SA 3.0

反射镜方程

像距、物距和镜子的焦距之间的相关性由一个称为反射镜方程的数学表达式指定。该方程也称为反射镜公式。

$$\mathit{\frac{1}{v}+\frac{1}{u}=\frac{1}{f}}$$

上述方程适用于凹面镜和凸面镜以及所有物距。使用反射镜方程时，务必使用符号约定。

使用此方程时，凸面镜的焦距取正值，而凹面镜的焦距取负值。

反射镜方程中使用的术语

在反射镜方程中使用的术语如下：

• u 是物体到镜子的距离。

• v 是像到镜子的距离。

• f 是焦点到镜极的距离。

镜子的用途

镜子是一项伟大的发明，它使我们的生活更加便利。它们在我们的日常生活中以多种方式使用，如下所示：

• 平面镜用于太阳灶中反射照射在其上的阳光。

• 平面镜用于在准备就绪时照看自己。

• 凹面镜用于手电筒、车前灯和闪光灯。

• 牙医使用球面凹面镜来获得放大的口腔图像。

• 在车辆中，凸面镜用作后视镜，以获得更宽阔的车辆后方道路视野。

• 凹面镜用于显微镜中放大样品图像，也用于望远镜中反射遥远的星体。

• 放大镜使用两个凸面镜。

• 凸面镜放置在道路和停车场的急转弯处，以获得更好的视野。

结论

在本教程中，解释了一个非常重要的光学物理概念，通过该概念我们可以理解镜子的用途及其在生活中的重要性。不同形状的镜子用于不同的目的，为了获得所需的成像，使用带符号约定的反射镜方程或反射镜公式。

常见问题

1. 反射镜方程能否写成 f=v+u？

$$\mathrm{ 我们知道反射镜方程是 \mathit{\frac{1}{f}=\frac{1}{v}+\frac{1}{u}}}$$

$$\mathrm{现在解上述方程，\mathit{\frac{1}{f}=\frac{vu}{v+u}}}$$

为了获得 f 的值，上述方程可以写成

$$\mathit{f=\frac{v+u}{vu}}$$

这是唯一可以写出反射镜方程的方式。因此，反射镜方程不能写成 f=v+u。

2. 讨论反射镜方程的应用。

反射镜方程的应用包括：

• 如果给出焦距和物距，则用于求像距。

• 当已知像距和焦距时，它也可以求出物距。

• 如果给出像距和物距，则使用此方程可以得到镜子的焦距。

3. 定义镜子的主焦点。

当与光轴等距的光线照射到空心球面镜的一部分时，反射后会在同一轴上汇聚到一个点或发散到一个点。这个点称为主焦点。

4. 凹透镜和凹面镜有什么区别？

将物体放置在镜子前面并且靠近镜子时会形成放大的图像，而当放置在与镜子有一定距离时会形成倒立的图像，而凸面镜在物体的任何位置都只会产生较小的正立图像。

5. 透镜与镜子的区别是什么？

镜子和透镜的区别如下：

序号	镜子	透镜
1.	一块玻璃的一部分，其中一个表面涂银，另一个表面用于反射光。	它是一块透明的玻璃，周围有两个表面，其中一个表面是弯曲的。
2	它是弯曲的或平面的。	它的一侧或两侧都是弯曲的。
3	它由玻璃或金属制成。	它由玻璃或塑料制成。
4	它基于反射定律的原理。	它基于折射定律的原理。
5	反射镜方程由 −$$\mathit{\frac{1}{f}=\frac{1}{v}+\frac{1}{u}}$$给出	透镜公式由 − $$\mathit{\frac{1}{f}=\frac{1}{v}-\frac{1}{u}}$$给出