球面镜公式

---

引言

光是电磁辐射，是电磁波谱中唯一可见于人眼的部分。如果光照射任何表面，表面接收到的光量取决于光源与表面的距离。照明定律或反平方照明定律给出了光源和表面之间的关系。它解释了表面照明随光源与表面之间距离平方的变化。当光照射粗糙表面时，它可以向各个方向散射。但是对于抛光表面，由于光的反射，会在特定角度看到合适的照明。

什么是镜子？

镜子是用来观察物体和生物图像的物体。如果物体放置在镜子前面，光线会从镜面反射，并在镜子上形成物体的图像。镜子就像水一样，显示其前面物体的图像。这是通过在镜子背面喷涂一层薄薄的铝或银来实现的。因为它们具有高反射率。因此，照射到镜子上的光线会在镜子的背面反射。

镜子的类型

根据镜子的形状，镜子分为平面镜和球面镜。

平面镜

平面镜是一块薄而平坦的玻璃，其背面涂有金属。在平面镜中，像的大小和物体的尺寸相同。平面镜可以形成虚像和实像。如果平面镜以特定角度θ放置，则可以产生物体的多个图像。这是万花筒中使用的原理。平面镜具有无限大的曲率半径和焦距。像的成像距离与物体到平面镜的距离相似。平面镜成的像是正立的、虚的和倒置的。(此处“倒置”可能需要根据上下文调整，平面镜成像并非真正意义上的倒置，而是左右反转)

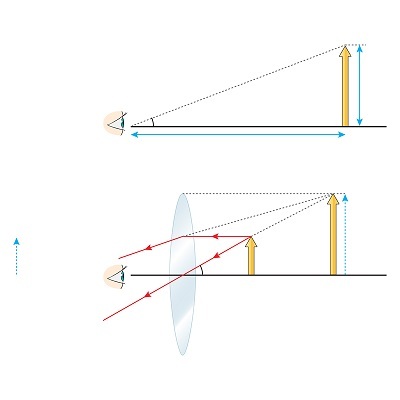
平面镜成像

球面镜

这些镜子是高度抛光的表面，切割成球体的一部分。球面镜的一侧是反射面，另一侧是镀银的。球面镜的中间部分是极点。球面镜的中心是曲率中心。球面镜的半径是曲率半径。球面镜的主轴是由连接极点和曲率中心的直线形成的。焦距是从极点到焦点测量的距离。

球面镜的类型

球面镜有两种类型：凹面镜和凸面镜。

凹面镜

光线从镜子的弯曲表面反射的球面镜被称为凹面镜。其外侧镀银，另一侧抛光。凹面镜可以产生虚像和实像。像的大小取决于物体与镜子之间的距离。

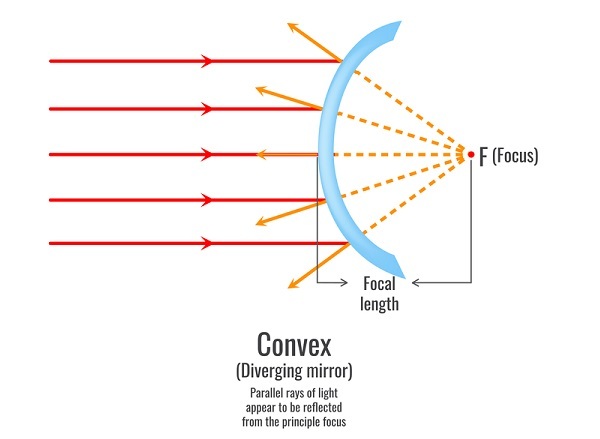
凸面镜

光线从镜子的曲面或凸出向外的镜面反射的球面镜称为凸面镜。凸面镜的另一个名称是发散镜。这些镜子形成的图像始终是虚的、缩小的和正立的。

镜面公式推导

镜面公式或镜面方程给出了物体和像与焦距之间的关系。镜面方程适用于平面镜和球面镜。镜面公式表示为

$$\mathit{\frac{1}{f}=\frac{1}{v}+\frac{1}{u}}$$

f 表示镜子的焦距。u 表示像距。v 表示物距。

与入射光相同方向测量的距离记为正，与入射光方向相反测量的距离记为负。让我们考虑一个位于凹面镜主轴上的物体 AB，它产生一个实像。像形成在曲率半径和焦点之间。

$$\mathrm{设\: AB=h_o ,A'B'=h_i,FP=f,BP=u ,B'P=v and PC=R,}$$

$$\mathrm{根据假设\: \mathit{\frac{h_o}{h_i} =\frac{u-2f}{2f-v}}……………………………….(1)}$$

$$\mathrm{此外, \mathit{\frac{h_o}{h_i} =\frac{f}{v-f}}………………………………….(2)}$$

$$\mathrm{由方程 \:(1)\: \&\: (2)\:\:\: \mathit{\frac{f}{v-f}=\frac{u-2f}{2f-v}}}$$

$$\mathit{2f^2-vf=uv-2vf-uf+2f^2}$$

$$\mathit{uv-vf-uf=0}$$

$$\mathit{uv=uf+vf}$$

$$\mathrm{将方程除以\:uvf, }$$

$$\mathit{\frac{1}{f}=\frac{1}{v}+\frac{1}{u}}$$

符号约定

• 物体放置在镜子的左侧。

• 在主轴上方测量的物体高度记为正，在主轴下方测量的物体高度记为负。

• 在极点右侧测量的距离取为正，在左侧测量的距离取为负。

• 距离通常从极点测量。

结论

每当光线照射到镜面时，它都会被反射或折射。折射和反射的方式也取决于镜子的类型。在本教程中，讨论了关于镜子、球面镜和镜子类型的相关知识。还详细讨论了镜面公式的推导和符号约定。

常见问题

1. 反射定律是什么？

反射定律如下所示：

• 照射到表面的光线为入射光，从表面反射的光线称为反射光。

• 一条假想的线，垂直于入射点处的反射面，称为法线。

• 入射角等于反射角。

2. 凹面镜的用途是什么？

凹面镜具有多种用途。它用于汽车前灯、手电筒、闪光灯、探照灯、牙科镜子、检眼镜、太阳能熔炉、望远镜、显微镜、剃须镜和化妆镜。

3. 区分正反射和漫反射。

正反射	漫反射
光滑表面发生正反射	粗糙表面发生漫反射
反射光线是有规律的。	反射光线是不规则的。
可以观察到反射。	无法观察到反射。

4. 什么是放大率？

像的大小与物体大小的比例称为镜子的线性放大率。它表示为 m。

$$\mathrm{放大率 (m)=\frac{像高}{物高}}$$

5. 凸面镜的用途是什么？

• 它用于建筑物的走廊和车辆的后视镜。

• 它用于道路弯道和转弯以及盲点。