非负矩阵分解

---

介绍

非负矩阵分解 (NMF) 是一种监督算法，用于将数据表示为更低的维度，这减少了特征的数量，同时保留了足够的基本信息，以便从降低的特征空间中构建原始矩阵。

在本文中，我们将进一步探讨 NMF 及其用途。

非负矩阵分解

NMF 用于降低输入矩阵或语料库的维度。它使用因子分析，对不太相关的词语给予较少的重视。因此，原始矩阵（非负矩阵）的分解产生了两个非负系数的乘积，其秩低于原始矩阵。

NMF 的重要性

• NMF 属于用于确定隐藏状态的基于代数的算法类别。

• 它可以用于主题建模 TF-IDF。

• NMF 可以轻松提取稀疏数据和因子。

以下是主题建模中非负矩阵分解的表示

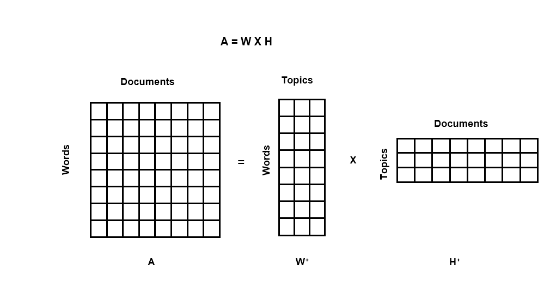
矩阵 1 (H+)：主题和词语

矩阵 3 (W+)：文档和主题

NMF 的表示

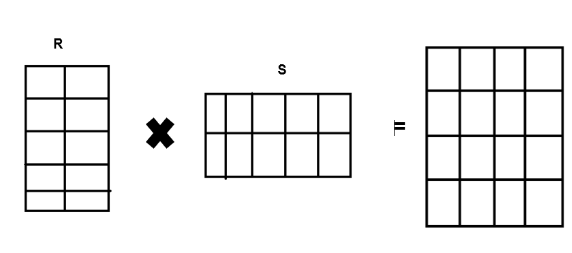
让我们有一个形状为 p x q 的输入矩阵 M。矩阵分解主题建模将把矩阵 M 分解成两个形状为 p x t 和 t x q 的矩阵 R 和 S。

因此，我们有如下所述的三个矩阵。

矩阵 M - 形状 (p x q) 表示文档词矩阵

矩阵 R - 形状 (p x t) 表示词嵌入矩阵

矩阵 S - 形状 (t x q) 每个句子中每个词的权重在每一列中表示

NMF 的数学建模

NMF 是一种无监督的机器学习技术，用于计算元素之间的距离。有多种方法可以计算距离。下面讨论了两种这样的方法。

• KL 散度 - 它用于确定两个分布在定量方面的接近程度。因此，如果两个词语相似且接近，则 KL 散度的值趋于零，否则它会增加。

KL 散度的通用公式如下所示

$$\mathrm{D_{K\:L}(p(x)||q\left ( x \right ))=\sum _{x\epsilon X}p(x)ln\frac{p(x)}{q(x))}}$$

• 欧氏距离 - 空间中两点之间的距离可以表示为

$$\mathrm{d(p,q)=\sqrt{(q_{1}-p_{1})^{2}+(q_{2}-p_{2})^{2}}}$$

非负矩阵分解的优点

• 在最小化成本函数的同时，它可以处理缺失数据，并且不将缺失数据视为零。

• 它可以通过将更高复杂度的矩阵分解为低维矩阵来工作。它被认为比 LDA 更好。

结论

非负矩阵分解是一种广泛使用的降维技术，尤其是在与自然语言和机器学习相关的领域。它比 LDA 等竞争对手更快、更容易且产生更好的结果。