一对一函数

---

介绍

一对一函数是指将值域的每个元素映射到其定义域中的一个元素的函数。函数定义为一组输入与其各自输出之间的关系。简单来说，函数是输入之间的关系，其中每个输入都与一个输出相关联。每个函数都有一个定义域和一个陪域或值域。函数通常用𝑓(𝑥)表示，其中x是输入。

函数的一般表示形式为

$$\mathrm{y\:=\:f(x)}$$

从数学角度来看，这些关系可以描述为一对一函数。在这种情况下，元素的数量相同，或者一个元素只能与另一个元素配对。

在本教程中，我们将讨论一对一函数。

函数

函数是一种特殊的关系。数学函数通常被视为给出每个输入x的唯一输出的规则。映射或变换用于表示数学函数。这些函数通常用f、g和h等字母表示。定义域定义为您可以输入的所有值的集合，而函数可以被定义。值域包含作为问题中函数输出返回的所有值。陪域是一组可以作为函数输出输出的值。

每个函数都有一个定义域和一个陪域或值域。函数通常用𝑓(𝑥)表示，其中x是输入。

函数的一般表示形式为

$$\mathrm{y\:=\:f(x)}$$

函数类型

基于集合元素的不同类型的函数：

• 一对一函数

• 多对一函数

• 满射函数

• 一对一且满射函数

• 入射函数

• 常数函数

一对一函数

术语“一对一关系”实际上指的是任何两个对象之间的关系，其中一个对象只能与另一个对象相关联。从数学角度来看，这些关系可以描述为一对一函数。在这种情况下，元素的数量相同，或者一个元素只能与另一个元素配对。

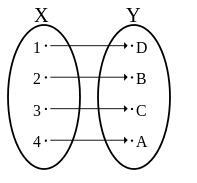
多对一函数

多对一函数由函数$\mathrm{f\:\colon\:A\rightarrow\:B}$定义，使得集合A的多个元素连接到集合B的相同元素。对于多对一特性，多个元素共享相同的陪域或像。如果陪域多对一函数只有一个值。

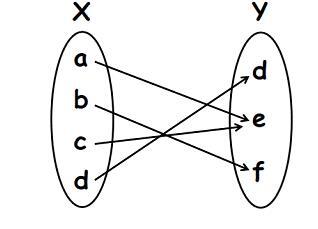
满射函数

在满射函数中，每个陪域元素都与定义域元素相关联。对于在A→B中定义的函数，集合B中的所有元素都具有集合A的原像。满射函数也称为满射函数。

一对一且满射函数

既是一对一函数又是满射函数的函数称为双射函数。在这里，定义域的每个元素都映射到陪域内的特定元素，并且陪域的每个元素都有一个原型（原像）。也就是说，集合A中的所有元素都与集合B中的特定元素相关联，集合B中没有剩余元素。

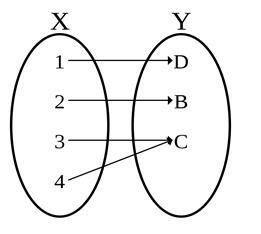
入射函数

就其属性而言，入射函数与满射函数完全相反。这里，末尾有一个特定的元素没有原像（原型）。集合B的元素是冗余的，并且与集合A的任何元素都不相关联。

常数函数

这些函数是多对一函数的一种重要形式。在常数函数中，每个定义域元素都只有一个像。

常数函数的格式为f(x) = K，其中K是一个实数。对于常数函数中不同值域的值（x值），获取相同值域中的K值。

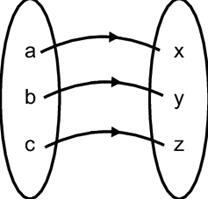
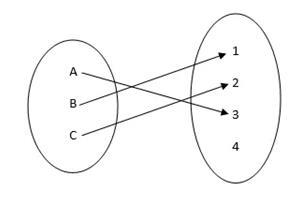
一对一（单射）函数

一对一（单射）函数是一种特殊的函数，它将值域的每个元素精确地映射到其定义域中的一个元素，即输出不会重复。一对一函数由f: X → Y定义，使得集合X的每个元素都与集合Y的特定元素相关联。一对一函数也称为单射函数。在这里，定义域的每个元素都有一个特定于特定函数的像或陪域元素。“一对一关系”一词实际上指的是任何两个对象之间的关系，其中一个对象只能与另一个对象相关联。从数学角度来看，这些关系可以描述为一对一函数。在这种情况下，元素的数量相同，或者一个元素只能与另一个元素配对。

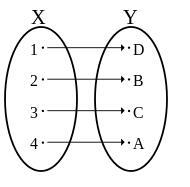
如何证明一个函数是一对一的

1. 证明函数是一对一或满射的最佳方法是使用定义。

如果对于每个𝑥, 𝑦 ∈ 𝐴，$\mathrm{f(x)\:=\:f(y)\:then\:x\:=\:y}$，则函数𝑓: 𝐴 → 𝐵被称为一对一（单射）函数。

这仅仅意味着A的唯一元素映射到B的唯一元素。让我们来看一下定义为$\mathrm{f(x)\:=\:2x\:+\:4}$的函数𝑓: 𝑅 → 𝑅。

现在我们需要证明它是一对一函数。

假设$\mathrm{f(x)\:=\:f(y)}$

这意味着$\mathrm{2x\:+\:4\:=\:2y\:+\:4}$

或$\mathrm{x\:=\:y}$

因此，根据定义，f(x)是一对一函数。

2. 水平线检验。

单射函数可以通过水平线检验或几何检验来确定。如果水平线只与函数图相交一次，则该函数是一对一的。

如果水平线与函数图相交多次，则该函数不是一对一的。

已解决的例子

1) 证明定义为$\mathrm{f(x)\:=\:6x\:+\:9}$的函数$\mathrm{f\colon\:R\rightarrow\:R}$是单射函数或一对一函数。

答案：给定定义为$\mathrm{f(x)\:=\:6x\:+\:9}$的函数$\mathrm{f\colon\:R\rightarrow\:R}$

现在我们需要证明它是一对一函数。

假设$\mathrm{f(x)\:=\:f(y)}$

这意味着$\mathrm{6x\:+\:9\:=\:6y\:+\:9}$

或$\mathrm{x\:=\:y}$

因此，根据定义，f(x)是一对一函数。

2) 如果𝑨 = {4, 5, 6}并且𝑩 = {p, q, r, s}，则以下哪个函数是一对一的。

$\mathrm{\lbrace\:(4\:,\:r)\:,\:(5\:,\:r)\:,\:(5\:,\:r)\rbrace\:}$

$\mathrm{\lbrace\:(4\:,\:p)\:,\:(5\:,\:r)\:,\:(6\:,\:s)\rbrace\:}$

$\mathrm{\lbrace\:(4\:,\:p)\:,\:(4\:,\:r)\rbrace\:}$

答案 - {(4, p),(5, r),(6, s)} 这是一个一对一函数。这是因为集合B的元素唯一地映射到集合A的元素。

3) 证明定义为$\mathrm{f(x)\:=\:x^{2}\:-\:2}$的函数$\mathrm{f\colon\:R\rightarrow\:R}$不是一对一函数。

答案 - 对于一对一函数$\mathrm{f(x)\:=\:f(y)}$

$$\mathrm{x^{2}\:-\:2\:=\:y^{2}\:-\:2}$$

$$\mathrm{\Longrightarrow\:x^{2}\:=\:y^{2}}$$

$$\mathrm{\:\:\:\:\:\:\:\:\Longrightarrow\:x^{2}\:-\:y^{2}\:=\:0}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:(x\:-\:y)\:(x\:+\:y)\:=\:0}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:x\:=\:y\:and\:x\:=\:-y}$$

由于我们在x和y中得到了两个关系𝑥 = 𝑦 𝑎𝑛𝑑 𝑥 = −𝑦，因此它不满足一对一函数的条件。

结论

术语“一对一关系”实际上指的是任何两个对象之间的关系，其中一个对象只能与另一个对象相关联。从数学角度来看，这些关系可以描述为一对一函数。在这种情况下，元素的数量相同，或者一个元素只能与另一个元素配对。

常见问题

1. 函数是什么意思？

函数是一种特殊的关系。数学函数通常被视为给出每个输入x的唯一输出的规则。

2. 一对一函数是什么意思？

术语“一对一关系”实际上指的是任何两个对象之间的关系，其中一个对象只能与另一个对象相关联。

3. 满射函数是什么意思？

在满射函数中，每个陪域元素都与定义域元素相关联。对于在A→B中定义的函数，集合B中的所有元素都具有集合A的原像。满射函数也称为满射函数。

4. 一对一且满射函数是什么意思？

既是一对一函数又是满射函数的函数称为双射函数。在这里，定义域的每个元素都映射到陪域内的特定元素，并且陪域的每个元素都有一个原型（原像）。

5. 多对一函数是什么意思？

多对一函数由函数$\mathrm{f\colon\:A\rightarrow\:B}$定义，使得集合A的多个元素连接到集合B的相同元素。对于多对一特性，多个元素共享相同的陪域或像。