Python Wand 中的 path_curve_to_quadratic_bezier() 函数
贝塞尔曲线是 Python 的内置绘图函数。它用于根据给定的点在 Python 中绘制曲线。
二次贝塞尔曲线是一个 Python 函数,它通过顶点(控制点)为二次贝塞尔曲线绘制路径。二次贝塞尔曲线是一个参数曲线,它定义了二维空间中的路径。该曲线由一个控制点和两个端点连接。
在可视化程序中,您可以使用此函数轻松构建和绘制。使用时间参数,您可以找到两个控制点并确定它们的位置。您可以通过这种方式构建敏感位置并将这些位置像曲线一样连接起来。借助此函数,我们可以轻松创建使用其他函数或方法难以或无法创建的曲线和形状。例如,借助二次贝塞尔函数,我们可以创建不同类型的图表和动画。
语法
此语法用于给定的示例:
def quadratic_bezier(p0, p1, p2, t):
这里 p0、p1 和 p2 代表点,t 代表值。
示例 1
在这个程序中,我们使用不同的点绘制曲线。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (0, 3) # beginning point
p1 = (4, 2) # Control point
p2 = (1, 8) # finishing point
t = 50
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
输出
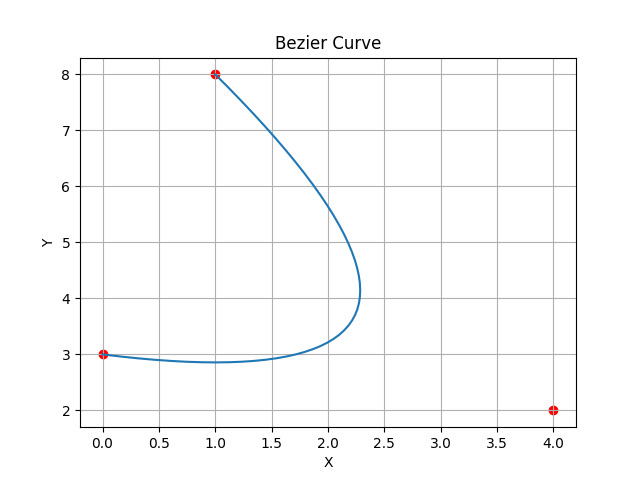
在此代码中,我们使用 matplotlib 和 numpy 创建了一个贝塞尔曲线。我们已定义并使用它来绘制在贝塞尔曲线上运行的点。起始点、控制点和结束点将显示在输出中。
示例 2
在这个程序中,我们使用不同的点绘制曲线。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (2, 3) # beginning point
p1 = (6, 5) # Control point
p2 = (3, 2) # finishing point
t = 50
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
输出
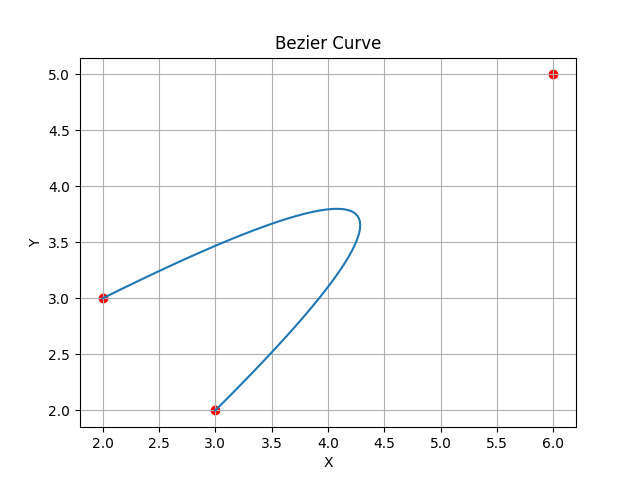
在此代码中,我们使用 matplotlib 和 numpy 生成了一个贝塞尔曲线。我们使用的方法定义并绘制了贝塞尔曲线上起始的点。输出将显示起始点、控制点和结束点。
示例 3
在这个程序中,我们使用不同的点绘制曲线。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (2, 3) # beginning point
p1 = (-2, 5) # Control point
p2 = (-3, 2) # finishing point
t = 80
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
输出
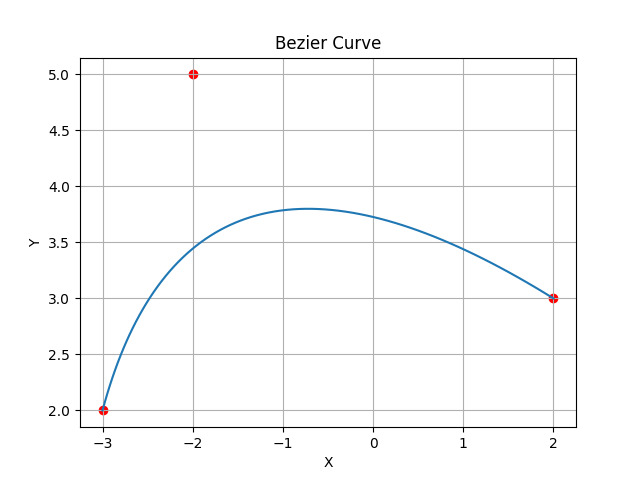
在此代码中,为了创建贝塞尔曲线,使用了 matplotlib 和 numpy。我们使用的方法定义并绘制了贝塞尔曲线上起始的点。输出或图表中将显示起始点、控制点和结束点。
示例 4
在这个程序中,我们使用不同的点绘制曲线。
import matplotlib.pyplot as plt
import numpy as np
def quad_bez(p0, p1, p2, t):
t1 = np.linspace(0, 1, t)
x = (1 - t1) ** 2 * p0[0] + 2 * (1 - t1) * t1 * p1[0] + t1 ** 2 * p2[0]
y = (1 - t1) ** 2 * p0[1] + 2 * (1 - t1) * t1 * p1[1] + t1 ** 2 * p2[1]
return x, y
p0 = (2, -5) # beginning point
p1 = (-2, 5) # Control point
p2 = (-3, 2) # finishing point
t = 50
x, y = quad_bez(p0, p1, p2, t)
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], c='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Bezier Curve')
plt.grid(True)
plt.show()
输出
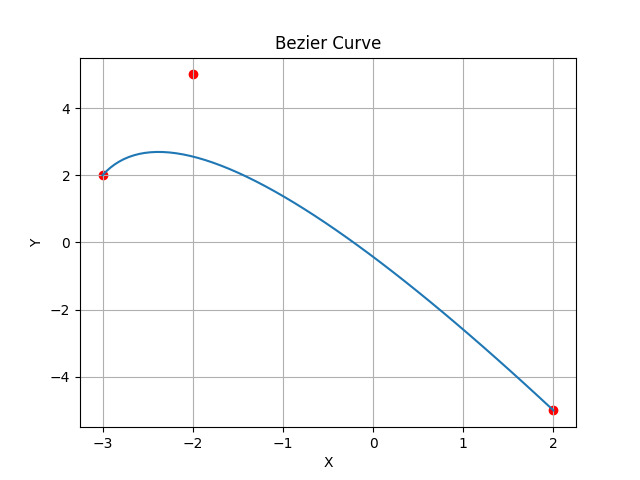
在此代码中,使用 matplotlib 和 numpy,我们构建了一个贝塞尔曲线。我们已经识别并使用了沿贝塞尔曲线的点。图像将显示起始点、控制点和结束点。
在上面的示例中,我们可以看到通过使用起始点、控制点和结束点创建的不同图表。
结论
总之,二次贝塞尔函数用于 Python Wand 创建平滑曲线。它需要三个点作为输入,并生成一条通过端点并受控制点位置影响的曲线。


 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP