数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学C语言程序中以矩阵对角线模式打印数字。
任务是打印nxn的对角线模式矩阵。
如果n为3，则以对角线模式打印矩阵为：
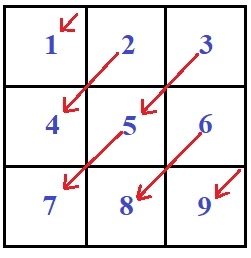
所以输出将类似于：
示例
Input: 3 Output: 1 2 4 3 5 7 6 8 9 Input: 4 Output: 1 2 4 7 3 5 8 11 6 9 12 14 10 13 15 16
问题表明我们必须给出一个数字n，生成一个nxn的矩阵，然后我们必须以对角线模式遍历矩阵并将值存储在单独的矩阵中。
但这会增加代码的复杂性，所以我们将：
创建一个大小为**N X N**的矩阵，用于存储打印前的模式。
将元素存储在模式的上三角中。观察到，当您沿对角线向下移动时，行索引增加1，列索引减少1。
完成上三角后，以与上三角类似的方式存储下三角的元素，即当您沿对角线向下移动时，行索引增加1，列索引减少1。
算法
int printdiagonal(int n) START STEP 1: DECLARE int mat[n][n], i, j, k, d=1, m STEP 2: LOOP FOR i = 0 AND i < n AND i++ ASSIGN j AS i AND k AS 0 LOOP FOR j = I AND j >= 0 AND j-- ASSIGN mat[k][j] AS d INCREMENT d AND k BY 1 END LOOP END LOOP STEP 3: LOOP FOR k = 1 AND k < n AND k++ ASSIGN i AND m EQUALS TO k LOOP FOR j = n-1 AND j >= m AND j-- ASSIGN mat[i][j] AS d; INCREMENT d AND i WITH 1 END FOR END FOR STEP 4: LOOP FOR i = 0 AND i < n AND i++ LOOP FOR j = 0 AND j < n AND j++ PRINT mat[i][j] END FOR PRINT NEWLINE END FOR STOP
示例
#include <stdio.h>
int printdiagonal(int n){
int mat[n][n], i, j, k, d=1, m;
for ( i = 0; i < n; i++){
j = i;
k = 0;
for ( j = i; j >= 0; j--){
mat[k][j] = d;
d++;
k++;
}
}
for ( k = 1; k < n; k++){
i = m = k;
for ( j = n-1; j >= m; j--){
mat[i][j] = d;
d++;
i++;
}
}
for ( i = 0; i < n; i++){
for(j = 0; j < n; j++){
printf("%d ", mat[i][j] );
}
printf("
");
}
}
int main(int argc, char const *argv[]){
int n = 3;
printdiagonal(n);
return 0;
}输出
如果我们运行上面的程序，它将生成以下输出：
1 2 4 3 5 7 6 8 9
更新于：2019年8月22日
2K+ 次浏览
广告