数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究构建DFA以检查给定整数是否为无符号整数的程序
在这个问题中，我们需要使用DFA来检查给定的数字是否为无符号整数。我们需要使用二维数组构建DFA来解决问题。
问题陈述 – 我们给定长度为N的字符串str。通过构建DFA，我们需要检查str是否表示无符号整数。在输出中，根据数字是否为无符号整数打印“无符号整数”或“不是无符号整数”。
示例
输入– str = "1729"
输出– “无符号整数。”
解释– 由于数字不包含任何符号，因此它是无符号整数。
输入– str = “-1729”
输出– “不是无符号整数。”
解释– 该数字在开头包含一个符号，因此它不是无符号整数。
方法1
在开始解决问题之前，让我们了解如何构建DFA来查找无符号整数。
以下是一些无符号整数的示例。
1234
1234.4567
1234E+215
1234E-215
123.456e+215
123.456e+215
以上示例表明，无符号整数可以包含数字、点、E/e、+ 或 -，以及再次出现的数字。
现在，让我们构建DFA，如下所示。
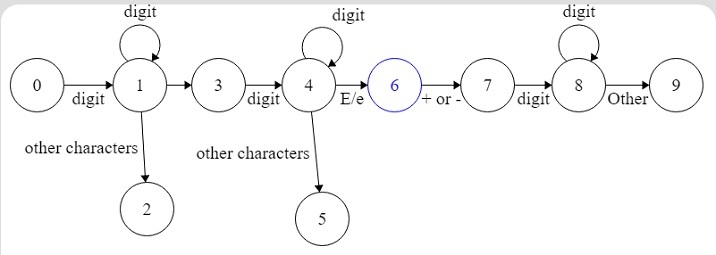
在上面的DFA中，我们从第0个状态开始。数字可以以任何数字开头，并包含多个数字，因为我们移动到第1个状态。
在第1个状态之后，如果我们得到其他字符，我们可以移动到第2个状态；如果我们在十进制数中得到“.”，则可以移动到第3个状态。
在第3个状态之后，我们需要至少1个或多个数字，然后我们可以移动到第4个状态。
从第4个状态，如果我们得到其他字符以接受数字，我们可以移动到第5个状态；如果我们得到E/e，则可以移动到第5个状态。
如果在E/e之后得到“+”或“-”，我们可以进入第6个状态。这里，E/e表示指数；之后，我们需要写正或负幂。
之后，我们需要以数字添加幂。因此，我们可以移动到第8个状态。
如果从第8个状态得到任何字符，我们可以移动到第9个状态。
现在，我们需要在代码中构建DFA。
在二维数组中，第一维表示当前状态，第二维表示字符类型，如下所示。
第0个索引用于数字。
第1个索引是“+/-”符号。
第2个索引是“.”。
第3个索引用于其他字符。
第4个索引是“e/E”。
方法
定义“digits”字符串并添加所有数字。另外，定义“sign”、“dot”和“ex”变量，并用各自的值初始化它们。
定义“dfa”数组以存储状态和下一个状态。另外，定义constructDFA()函数以使用二维数组构建DFA。
在constructDFA()函数中，用“10”初始化数组，因为最初所有状态都无法访问。
我们需要根据下一个状态更新数组的值。例如，最初，我们处于状态0，并且只有当字符串以数字开头时才能继续前进。因此，更新dfa[0][0] = 1。
在isUnsignedInt()函数中，首先执行constructDFA()函数以构建DFA。
用0初始化“current_state”变量以跟踪状态。
开始遍历字符串。
现在，通过从二维数组中获取值来将“current_state”的值更新为下一个状态。例如，如果当前字符是数字，则使用dfa[current_state][0]更新“current_state”变量的值。如果当前字符是“+/-”符号，则使用dfa[current_state][1]更新current_state变量的值。
最后，如果“current_State”的值为1、4或8。这意味着给定的数字是有效的无符号整数。
示例
#include "bits/stdc++.h"
using namespace std;
string digits = "0123456789", sign = "+-";
string dot = ".", ex = "eE";
int dfa[11][5];
// function to construct DFA
void constructDFA() {
// Initially, all states are unreachable from state 0, so connect all states to state 10 (dead state).
for (int i = 0; i < 11; i++)
for (int j = 0; j < 5; j++)
dfa[i][j] = 10;
// If the state is zero and we get a digit, then change the state to 1.
dfa[0][0] = 1;
// If the state is 1, and we get different characters, set the array value accordingly.
dfa[1][0] = 1;
dfa[1][2] = 3;
dfa[1][3] = 2;
dfa[1][4] = 6;
// Also, Initialize the array value for states 3, 6, 7, 8.
dfa[3][0] = 4;
dfa[4][0] = 4;
dfa[4][3] = 5;
dfa[4][4] = 6;
dfa[6][0] = 8;
dfa[6][1] = 7;
dfa[7][0] = 8;
dfa[8][0] = 8;
dfa[8][3] = 9;
}
// function to check if the given string is an unsigned integer or not
string isUnsinedInt(string s) {
// Build the DFA
constructDFA();
// Initially, the current state is 0.
int current_state = 0;
// Traverse the string
for (int i = 0; i < s.size(); i++) {
// Check the type of the current character and change the state accordingly
// If a digit occurs
if (digits.find(s[i]) != digits.npos)
// Change the state to 0.
current_state = dfa[current_state][0];
// If a sign occurs, change the state to 1.
else if (sign.find(s[i]) != sign.npos)
current_state = dfa[current_state][1];
// If a dot occurs, change the state to 3.
else if (dot.find(s[i]) != dot.npos)
current_state = dfa[current_state][2];
// If e/E or exponent sign occurs, change the state to 4.
else if (ex.find(s[i]) != ex.npos)
current_state = dfa[current_state][4];
// If any other character occurs, change the state to 3.
else
current_state = dfa[current_state][3];
}
// If the current state is 1, 4, 8, then the number is an unsigned integer
if (current_state == 1 || current_state == 4 || current_state == 8) {
return "Unsigned integer";
}
else {
return "Not an unsigned integer";
}
}
int main() {
string str = "1729";
cout << "The given number is " << isUnsinedInt(str);
return 0;
}
输出
The given number is Unsigned integer
时间复杂度 – O(N)，因为我们遍历字符串。
空间复杂度 – O(1)，因为我们使用常量空间来存储DFA状态。
在本教程中，我们构建了DFA来检查给定的字符串是否为无符号整数。此外，程序员可以通过给定的图像可视化DFA，并更好地理解DFA。之后，我们使用二维数组构建了相同的DFA。为了获得结果，我们根据当前字符更改“current_state”的值以获取下一个状态。程序员可以尝试解决其他包含DFA构建的问题。
218 次浏览
