Python程序：计算包含给定边的唯一路径数量

假设我们有一组边，格式为 (u, v)，它们表示一棵树。对于每条边，我们必须找到包含该边的所有唯一路径的数量，顺序与输入中给出的顺序相同。

例如，如果输入是 edges = [[0, 1],[0, 2],[1, 3],[1, 4]]

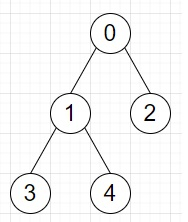
则输出将为 [6, 4, 4, 4]。

为了解决这个问题，我们将遵循以下步骤：

  • adj := 从给定边生成的邻接表

  • count := 一个空的映射

  • 定义一个函数 dfs()。它将接收 x, parent 作为参数。

  • count[x] := 1

  • 对于 adj[x] 中的每个邻居 nb：

    • 如果 nb 与 parent 相同，则

      • 跳出循环

    • count[x] := count[x] + dfs(nb, x)

  • 返回 count[x]

  • 在主方法中执行以下操作：

  • dfs(0, -1)

  • ans := 一个新的列表

  • 对于 edges 中的每条边 (a, b)：

    • x := count[a] 和 count[b] 中的最小值

    • 将 (x *(count[0] - x)) 添加到 ans 的末尾

  • 返回 ans

示例

让我们来看下面的实现以更好地理解：

在线演示

from collections import defaultdict
class Solution:
   def solve(self, edges):
      adj = defaultdict(list)
      for a, b in edges:
         adj[a].append(b)
         adj[b].append(a)
      count = defaultdict(int)
      def dfs(x, parent):
         count[x] = 1
         for nb in adj[x]:
            if nb == parent:
               continue
            count[x] += dfs(nb, x)
         return count[x]
      dfs(0, -1)
      ans = []
      for a, b in edges:
         x = min(count[a], count[b])
         ans.append(x * (count[0] - x))
      return ans
ob = Solution()
edges = [
   [0, 1],
   [0, 2],
   [1, 3],
   [1, 4]
]
print(ob.solve(edges))

输入

[
   [0, 1],
   [0, 2],
   [1, 3],
   [1, 4]
]

输出

[6, 4, 4, 4]

更新于：2020年12月22日

288 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告