Python扩展欧几里德算法程序
在本文中,我们将了解下面给出的问题陈述的解决方案。
问题陈述 − 给定两个数,我们需要计算这两个数的最大公因数并显示它们。
两个数的最大公因数(Greatest Common Divisor)是可以整除这两个数的最大值。这里我们遵循欧几里得方法来计算最大公因数,即重复除以这些数并且在余数为零时停止。这里我们根据递归中获得的先前值扩展算法。
现在让我们在下面的实现中观察解决方案 −
示例
# extended Euclidean Algorithm
def gcdExtended(a, b, x, y):
# Base Case
if a == 0 :
x = 0
y = 1
return b
x1 = 1
y1 = 1 # storing the result
gcd = gcdExtended(b%a, a, x1, y1)
# Update x and y with previous calculated values
x = y1 - (b/a) * x1
y = x1
return gcd
x = 1
y = 1
a = 11
b = 15
g = gcdExtended(a, b, x, y)
print("gcd of ", a , "&" , b, " is = ", g)输出
gcd of 11 & 15 is = 1
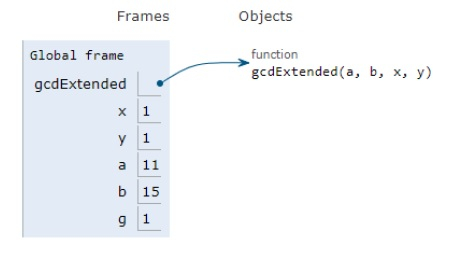
所有变量都在局部范围内声明,并且它们的引用在上图中可见。
结论
在本文中,我们学习了如何进行Python扩展欧几里得算法编程。

广告

 数据结构
数据结构 网络
网络 RDBMS
RDBMS 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C编程
C编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP