Python 语言第 n 个 Catalan 数

在本文中，我们将学习如何计算第 n 个 Catalan 数。

Catalan 数是自然数序列，由递归公式定义：−

$$C_{0}= 1\:and\:C_{n+1}=\displaystyle\sum\limits_{i=0}^n C_{i}C_{n-i} for \:n\geq0;$$

对于 n = 0, 1, 2, 3, …，前几个 Catalan 数为1, 1, 2, 5, 14, 42, 132,429,...................

Catalan 数既可以通过递归获得，也可以通过动态规划获得。下面让我们看看它们的实现方式。

方法 1： 递归方法

示例

 演示

# A recursive solution
def catalan(n):
   #negative value
   if n <=1 :
      return 1
   # Catalan(n) = catalan(i)*catalan(n-i-1)
   res = 0
   for i in range(n):
      res += catalan(i) * catalan(n-i-1)
   return res
# main
for i in range(6):
   print (catalan(i))

输出

1
1
2
5
14
42

所有变量和递归调用的范围如下所示。

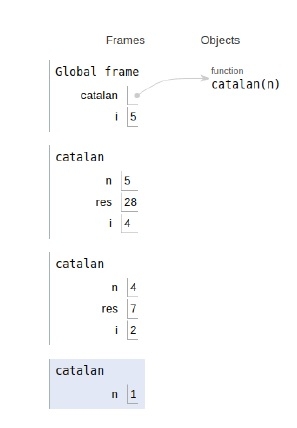
方法 2：动态规划方法

示例

 演示

# using dynamic programming
def catalan(n):
   if (n == 0 or n == 1):
      return 1
   # divide table
   catalan = [0 for i in range(n + 1)]
   # Initialization
   catalan[0] = 1
   catalan[1] = 1
   # recursion
   for i in range(2, n + 1):
      catalan[i] = 0
      for j in range(i):
         catalan[i] = catalan[i] + catalan[j] * catalan[i-j-1]
   return catalan[n]
# main
for i in range (6):
   print (catalan(i),end=" ")

输出

1
1
2
5
14
42

所有变量和递归调用的范围如下所示。

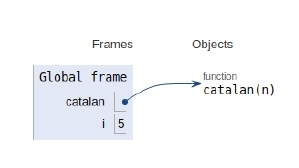
结论

在本文中，我们了解了生成第 n 个 Catalan 数的方法。

更新于： 2019 年 9 月 11 日

341 次浏览

开启您的职业生涯

通过完成课程获得认证

开始
广告