数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学C/C++程序计算第n个卡塔兰数？
卡塔兰数是一个数列。卡塔兰数构成一系列自然数，出现在各种计数问题中，通常涉及递归定义的对象。
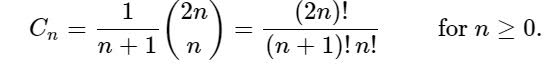
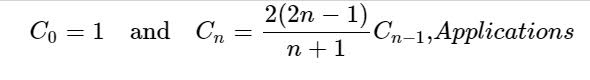
Cn是长度为2n的Dyck词的个数。Dyck词是一个由n个X和n个Y组成的字符串，其任何初始段的Y的个数都不超过X的个数。例如，以下是长度为6的Dyck词：
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.
将符号X重新解释为左括号，将Y解释为右括号，Cn计算包含n对正确匹配的括号的表达式的个数。
((())) ()(()) ()()() (())() (()())
Cn是n+1个因子可以完全括号化的不同方法的个数（或应用二元运算符的n种关联方法的个数）。例如，对于n=3，我们有以下五种不同的四因子括号化方法：
((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))
二元运算符的连续应用可以用满二叉树表示。（如果每个顶点要么有两个子节点，要么没有子节点，则根二叉树是满的。）因此，Cn是具有n+1个叶节点的满二叉树的个数。
示例
输入 - 6
输出- 1 1 2 5 14 42
解释
对于n = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...，前几个卡塔兰数是：
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,
示例
#include<iostream>
using namespace std;
long int catalan( int n) {
if (n <= 1){
return 1;
}
long int result = 0;
for (int i=0; i<n; i++){
result += catalan(i)*catalan(n-i-1);
}
return result;
}
int main(){
for (int i=0; i<6; i++)
cout << catalan(i) << " ";
return 0;
}输出
1 1 2 5 14 42
更新于：2019年8月13日
501 次查看
广告