质点直线运动

---

引言

如果粒子的位置随时间和周围环境而变化，则该粒子的本体就被认为是运动的。从数学角度来看，运动可以用特定参考系中的位移、速度和加速度来描述。位移、速度和加速度严格限制在一个方向上。

什么是质点直线运动？

运动是我们日常生活中的一种重要现象，主要体现在各种电子设备中。质点直线运动主要在坐标轴上适用。简单来说，质点直线运动主要用于对粒子运动进行适当的描述 (Nyobe 等人，2021)。

从数学角度来看，线性运动以及质点直线运动是描述粒子运动最常用的方法。

质点直线运动的应用

质点直线运动的应用常见于公共场所的电梯中。此外，测量由于自由落体运动而产生的物体的重力也是质点直线运动的一个完美例子。

质点直线运动应用的其他重要方面常见于儿童滑梯以及通常以飞行方式观察到的行星运动，这也是质点直线运动的完美例子。为了维持和测量物体的速度，可以通过“具有非均匀加速度的直线运动”来测量。

图1：直线运动的应用

测量物体非均匀加速度的运动是速度变化的独特例子。速度是一种线性类型，完全随时间变化，这就是为什么直线穿过直线的原因。两种不同粒子的运动都属于特定中心力的作用，例如静电力，这很容易通过使用质点直线运动来测量力。

质点直线运动的类型

直线运动分为三种不同的类型：匀速运动，主要作用于零加速度；“匀加速运动”，主要指恒定的非零加速度；此外，属于非匀加速运动的运动是最重要的直线运动类型之一。这种运动是重力下的自由落体运动以及与弹簧粒子大规模连接的简谐运动。所有类型的直线运动都分别用于属于任何其他电气设备的不同电场或磁场的粒子中。“匀速直线运动”是指物体以恒定速度和零加速度运动的情况 (Kailasham & Khair, 2022)。“匀加速直线运动”可以出现在粒子以大于零的恒定加速度运动的情况下。最后，如果粒子以不一致的速度以及快速变化的加速度运动，“具有非均匀加速度的直线运动”就会发生。

质点直线运动的功能

距离和位移是一个重要的概念，主要适用于质点直线运动。这里，距离是指在旅途中由电运动覆盖的总长度。运动的位移可以定义为路径起始位置和最终位置之间的距离。

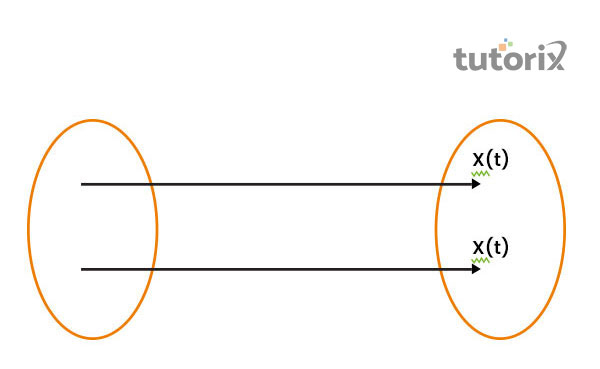
图2：质点直线运动

质点直线运动也常被称为直线运动，因为粒子是直线运动的。在上图中，x/(t) 表示沿运动方向移动的粒子的位置，公式中的 T 表示运动的初始时间 (Durey & Bush, 2021)。

在粒子的最终位置，时间是从运动的初始时间和最终时间计算出来的。质点直线运动主要用于测量粒子的位移、速度和加速度。

质点直线运动最常见的应用分别体现在许多不同数学问题的各种问题中。通过应用质点直线运动，粒子的位置和位移、速度以及运动学问题的评估主要接受导出的方程 (Schnitzer, 2022)。为了测量不同粒子的速度，质点直线运动经常被使用。

粒子的速度可以通过测量总行程距离乘以所用总时间来计算。通过应用质点直线运动，也可以通过从粒子的最终位置减去粒子的初始位置来测量粒子的速度，整个计算结果除以旅途中所用的总时间 (Diehl, 2020)。

• 电梯的运动是质点直线运动的一个完美例子。

结论

不同类型的运动都可以归类为质点直线运动。旋转运动是一种重要的运动类型，主要涉及特定物体的运动，该物体提供围绕旋转轴发生的圆周运动。这种特殊的运动通常通过地球的旋转来观察。振荡运动是另一个重要的类别，它反映了周期性运动。当孩子玩秋千时，通常会看到这种特殊的运动。

参考文献

期刊

Diehl, E. (2020). The Engineering Dynamics Course Companion, Part 1: Particles: Kinematics and Kinetics. Synthesis Lectures on Mechanical Engineering, 5(4), 1-245.

Durey, M., & Bush, J. W. (2021). Classical pilot-wave dynamics: The free particle. Chaos: An Interdisciplinary Journal of Nonlinear Science, 31(3), 033136. Retrieved from: https://aip.scitation.org

Kailasham, R., & Khair, A. S. (2022). Chaotic dynamics of an autophoretic particle. arXiv preprint arXiv:2203.01988. Retrieved from: https://arxiv.org

Nyobe, S., Campillo, F., Moto, S., & Rossi, V. (2021). The one step fixed-lag particle smoother as a strategy to improve the prediction step of particle filtering. Retrieved from: https://hal.inria.fr

Schnitzer, O. (2022). Weakly nonlinear dynamics of a chemically active particle near the threshold for spontaneous motion. Part 1: Adjoint method. arXiv preprint arXiv:2205.06136. Retrieved from: https://arxiv.org

网站

conceptualdynamics (2022), Different types of motion, Available at: http://www.conceptualdynamics.com [Accessed on 10th June 2022]