摄氏度和华氏度之间的关系

---

介绍

华氏和摄氏温标都具有重要的不同温度，水在这些温度下会结冰和沸腾。在摄氏温标上，温度用摄氏度表示。在另一个温标，即华氏温标上，温度主要用华氏度表示。

两种温标的历史和重要性

在华氏和摄氏温标之间，物理学家丹尼尔·盖布里埃尔·华伦海特于 1724 年首次发明了华氏温标。这位物理学家的主要研究方向是测量人体平均内部温度以及测量盐水结冰时的温度（Paoletti，2020）。

在华氏温标上，盐水（水、氯化铵和冰的溶液）在 0°F 时结冰。根据华伦海特的估计，人体内部的平均温度约为 90°F。后来，对人体内部温度的估计修正为 96°F，这非常接近真实的内部体温。

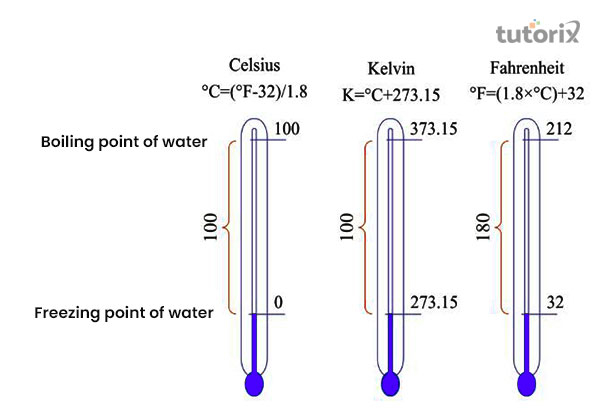
图 1：摄氏度和华氏度温度

摄氏温标由瑞典天文学家安德斯·摄尔修斯于 1742 年发明。目前的名称“摄氏温标”源于该温标发明者的名字。摄氏温标在其发明时主要用作 100 点系统（Sekerák 等人，2020）。

该温标最初用于测量水沸腾温度和雪融化温度之间的差异。“摄氏”一词来源于“centum”（意为 100）和“gradus”（意为度数或刻度）（Soria-Ruiz，2021）。

根据摄氏温标，水在 0°C 时结冰。根据摄氏温标，水的沸腾温度为 100°C。由于这两个温度之间的差异为 100 度，因此该温标的另一个名称是“百分温标”。

华氏和摄氏的单位

有两个不同的单位可以分别识别这两个不同的温度。每个温标的每一步都由不同的单位确定。摄氏温标的用户使用 °C 作为该温标的温度单位。华氏温标的用户使用 °F 来表示华氏温标测量的温度。

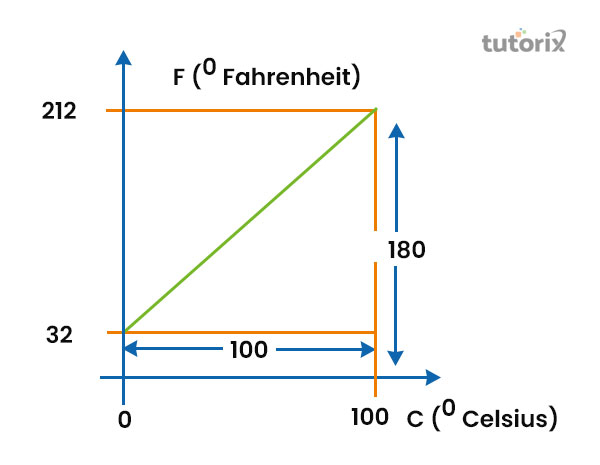
图 2：华氏度之间的关系

这两个温标之间的关系

摄氏和华氏温标之间存在重要的关系，因为这两个温标被广泛用于测量液体、人体和其他物质的温度。这两个温标之间的比例关系呈现出一个重要的事实。如果在特定温标上增加温度度数，则如果在另一个温标上测量，温度也会增加（Huda，2021）。因此，如果发现某物的温度在华氏温标上降低，则摄氏温标的温度也会降低。

温标名称	冰点	沸点
摄氏	0°C	100°C
华氏	32°F	212°F

表 1：华氏和摄氏温标之间的关系

摄氏度转换为华氏度

可以给出重要的公式，有助于将温度值从摄氏度转换为华氏度。此转换过程的公式为“F= (9/5*C) + 32”。在这个公式中，F 是华氏温标上的温度值，C 是要转换为华氏度的摄氏温标上提供的温度值的代表（Yaffe，2022）。例如，如果有人想获得 51°C 的华氏值，可以使用以下公式。

C 的值 = 51°C

F = (9/5*51) + 32

F = 123.8°F

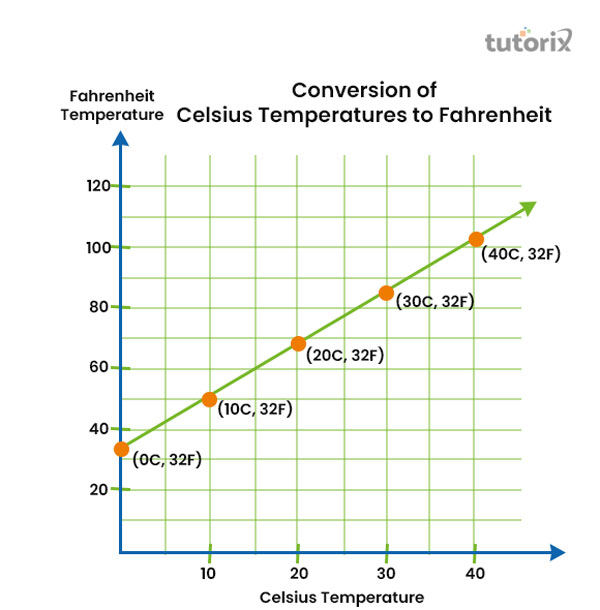
图 3：摄氏温度转换为华氏温度

如果华氏温标的温度升高，则摄氏温标的温度也会升高。例如，温度从 0°C 升高到 10°C，因此华氏温标上的温度也从 32°F 升高到 50°F（Hall，2020）。相反，30°C 升高到 40°C 会导致温度从 86°F 升高到 104°F。

华氏度转换为摄氏度

将华氏温度转换为摄氏度的公式为“C= 5/9 (F-32)”。在这个公式中，F 表示华氏温度值，C 表示摄氏度（Sjöberg 等人，2018）。例如，可以将 45°F 的值转换为华氏度。

华氏温标上的温度值：45°F

C= 5/9 (F-32)

C= 7.22

结论

全世界广泛使用摄氏温标来测量温度。在未来，摄氏测量将集中于测量水沸腾与结冰之间的差异。在那时，这两个温度将被放置在冷热光谱的两端。

常见问题

Q1. 摄氏温标的主要依据是什么？

水的冰点和沸点被认为是使用摄氏温标测量温度的主要依据。根据此温标，冰点为 0°C，水在 100°C 时开始沸腾。

Q2. 1°C 在华氏温标上的值是多少？

根据将摄氏值转换为华氏温标的公式，1°C 等于 33.8°F。此基本值有助于计算该温标的其他值。

Q3. 摄氏和华氏温标之间存在什么样的关系？

在摄氏和华氏温标之间可以找到比例关系。温度在一个温标上的值增加时，在另一个温标上的值也以相同的方式变化。

Q4. 测量温度最重要的三个温标是什么？

两个最重要的温标是摄氏和华氏温标。除了这两个温标之外，开尔文温标也是近来用于测量温度的另一个温标。

Q5. 除了摄氏和华氏之外，还有其他温度单位吗？

除了摄氏和华氏之外，牛顿、罗默、兰金、狄塞尔和摄尔修斯等都是其他单位。开尔文是用于测量温度的国际单位制单位。

参考文献

期刊

Hall, B. D. (2020, June). 软件用于物理量计算。在 2020 年 IEEE 国际工业 4.0 和物联网计量研讨会（第 458-463 页）。IEEE。检索自：https://www.researchgate.net

Huda, N. (2021). 发现一个方程来解决所有类型温度计的温度转换问题（最佳实践发现学习模型）。在伊斯兰教育与和平国际研讨会（第 1 卷，第 414-424 页）。检索自：http://ejournal.uniramalang.ac.id

Paoletti, T. (2020)。关于数量之间关系的推理以重新组织反函数的含义：Arya 的案例。数学行为杂志，57，100741。检索自：https://www.sciencedirect.com

Sekerák, J.，Lukáč, S. 和 Doboš, J. (2020, July)。利用 Geogebra 在数学教学中培养探究技能以分析和确定变量之间的关系。在 EDULEARN20 会议论文集（第 6 卷，第 7 页）。

Sjöberg, C.，Nouri, J.，Sjöberg, R.，Norén, E. 和 Zhang, L. (2018, July)。通过 Scratch 进行小学数学教学。在教育与新学习技术国际会议，EDULEARN18 会议论文集（第 5625-5632 页）。于 2022 年 6 月 11 日检索自：https://www.researchgate.net

Soria-Ruiz, A. (2021)。价值与尺度：一些观察和建议。Organon F，28（3），596-625。检索自：https://run.unl.pt

Yaffe, P. (2022)。科学的运作：人类能否在科学文盲中生存？普遍性，2022 年（2 月），1-12。检索自：https://dl.acm.org

网站

Glossary.periodni (2022)。关于摄氏温标。检索自：https://glossary.periodni.com [检索日期：2022 年 6 月 10 日]

Physics.stackexchange (2022)。关于摄氏度到华氏度的混淆：为什么没有 1 比 x 的比率？检索自：https://physics.stackexchange.com [检索日期：2022 年 6 月 10 日]