数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
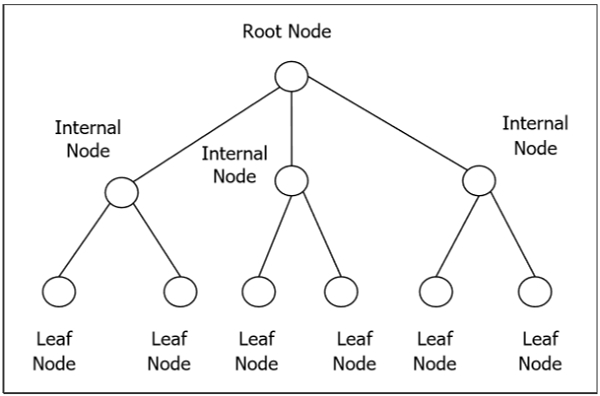
法学有根树和二叉树
有根树
有根树G是一个连通的无环图，它有一个特殊的节点称为树的根，并且每条边都直接或间接地起源于根。有序有根树是有根树，其中每个内部顶点的子节点是有序的。如果一个有根树的每个内部顶点最多有m个子节点，则称之为m叉树。如果一个有根树的每个内部顶点恰好有m个子节点，则称之为完全m叉树。如果m = 2，则有根树称为二叉树。
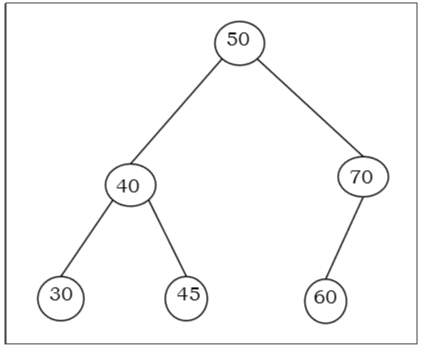
二叉搜索树
二叉搜索树是一种满足以下性质的二叉树：
- 顶点V的左子树中的X，Value(X) ≤ Value(V)
- 顶点V的右子树中的Y，Value(Y) ≥ Value(V)
因此，内部节点V的左子树的所有顶点的值都小于或等于V，内部节点V的右子树的所有顶点的值都大于或等于V。从根节点到最深节点的链接数是二叉搜索树的高度。
示例
在BST中搜索键的算法
BST_Search(x, k) if ( x = NIL or k = Value[x] ) return x; if ( k < Value[x]) return BST_Search (left[x], k); else return BST_Search (right[x], k)
二叉搜索树的复杂度
| 平均情况 | 最坏情况 | |
|---|---|---|
| 空间复杂度 | O(n) | O(n) |
| 搜索复杂度 | O(log n) | O(n) |
| 插入复杂度 | O(log n) | O(n) |
| 删除复杂度 | O(log n) | O(n) |
更新于：2019年8月26日
4K+ 次浏览
广告