旋转动能

---

简介

质心和延展物体的动能值可以用旋转动能来表示。线性动能和旋转动能都是基于功-能原理以平行的方式发展起来的。旋转动能的表示是基于物体旋转的特定轴线。

旋转动能：分析

在物体旋转期间，会产生旋转能量。总动能的一个重要部分被称为旋转能量。当旋转能量基于物体的旋转单独出现时，就会出现惯性矩。角动能是用来定义旋转能量的另一个术语（Cutting, Hindmarsh & Weir, 2020）。物体旋转的一个相关且有目的的结果是它的旋转能量。

图 1：旋转动能

旋转动能和转动惯量之间的关系本质上是成正比的。平方的大小也与角速度相关。旋转动能和平动能都存在于滚动物体中。

旋转动能的公式

可以通过遵循一个重要的公式来测量旋转物体及其旋转能量。用数学的方式，这个公式可以表示为 $\mathrm{K_R \:=\:1/2\: *I\: ω^{2}.}$ 在这个公式中，$\mathrm{K_R}$ 代表旋转动能的值 (Liu et al. 2018)。符号“I”表示惯性矩的值。公式中的 ω 表示角速度的值。

旋转动能是通过考虑惯性矩和角速度计算结果的一半来表示的。这个表达式可以用来表示动能的线性形式和旋转形式。功的原理与完成整个旋转所需的能量成正比。惯性矩和施加的扭矩之间的平行关系与此相关 (Zhao & Tresp, 2018)。作用在质量上的力用 m 表示。这是从正面和背面考虑的。

牛顿第二定律与旋转动能的关系

牛顿第二定律的概念与旋转动能的基础紧密相连。根据牛顿第二定律，加速度的值等于速度的合力值。速度值需要除以精确的时间量。

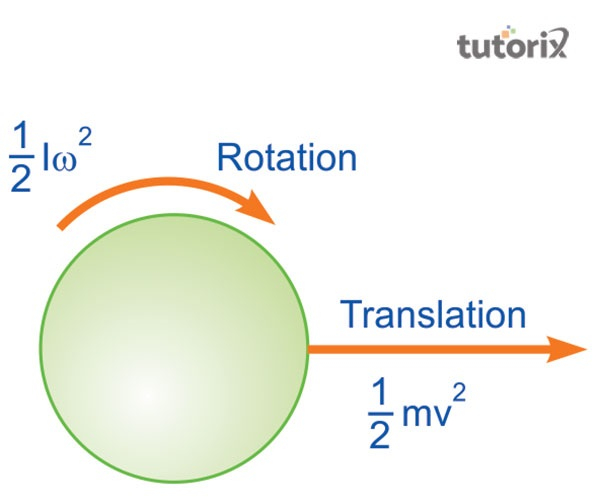
图 2：旋转目标

牛顿旋转第二定律很重要，因为从中可以提取角加速度的值。通过考虑最终速度结果的一半来提取平均速度值 (Zhang et al. 2020)。物体的旋转轴因物体而异。未连接的物体及其旋转轴围绕质心旋转。

旋转动能的相关单位

旋转动能在 SI 单位制中用 J（焦耳）表示。在 MKS 单位制中，该单位用 $\mathrm{kg.m^2.s^{-2}}$ 表示。通过呈现这一点，旋转动能值在维动能公式中表示。维公式也是一个重要的部分，可以用旋转动能的基本公式来表示。与惯性矩相关的维公式等于 $\mathrm{M^1L^2T^0}$。角速度也与此相关 (Ariska, Akhsan & Zulherman, 2018)。

它的维公式是 $\mathrm{M^0L^0T^{-1}}$。旋转动能的值可以通过减去角速度值和惯性矩的值来提取。这个减法的结果是 $\mathrm{M^1L^2T^{-2}}$。

旋转动能的特性

就任何其他物体而言，动能都更大。旋转动能可以转化为其他形式的能量。速度和动能之间存在着重要的关系。这种关系本质上是成正比的。随着物体速度的变化，动能会增加和减少 (Zhang et al. 2018)。旋转动能是用焦耳来测量和表示的。物体的方向与旋转动能紧密相关。旋转动能的使用帮助当地用户在使用正常过程中产生能量。

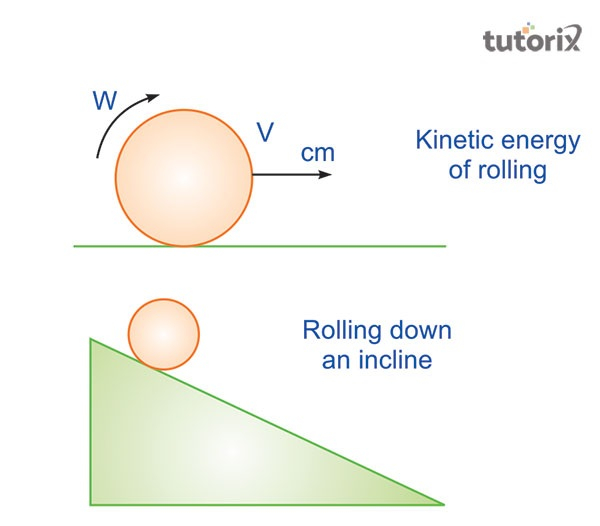
图 3：动能与滚动的关系

结论

在风力发电机中可以发现旋转动能，其中叶片由风力驱动。风击中叶片并使其旋转。叶片的这种运动有助于发电。在这种情况下，运动的空气具有动能。在这个过程中，动能被输出并转化为机械能。可以基于此分析功和能之间的关系。在万有引力和匀速圆周运动中，旋转动能也发挥着重要的作用。

常见问题

Q1. 旋转功率公式的意义是什么？

A1. 旋转功率公式很重要，因为它有助于提取动能的值。根据这个公式，还可以计算惯性矩的值。

Q2. 滚动物体中存在哪些类型的能量？

A2. 滚动物体是评估旋转动能的一个很好的例子。在这样的物体中，平动能和旋转动能都存在。

Q3. 测量惯性矩的单位是什么？

A3. 磁场强度单位被认为是测量惯性矩的合适单位。质量时间和距离是与惯性矩测量相关的两个重要因素。

Q4. 哪个因素会影响物体的旋转动能？

A4. 物体旋转的速度是旋转动能所依赖的主要因素。物体旋转得越快，能量水平就越高。质量的位置也是一个重要的因素。