动能和做功

---

简介

动能是与运动相关的能量。对于静止的物体，没有动能。在本文中，我们不讨论任何能量变化。例如，水被加热后转化为热能，从而变成蒸汽。我们可以在环境和日常生活中找到许多这样的能量变化，但它们不在本文的讨论范围之内。在这里，我们讨论与运动物体相关的动能。运动物体由于对其施加的力而获得动能，这可以用一个公式表示

$\mathrm{KE=\frac{1}{2}mv^2}$

但是功取决于施加在物体上的力和距离。所做的功是施加的力与物体移动距离的乘积。为了获得所覆盖的距离，必须做功。对吧？当我们只说“功”时，它是对需要做什么、需要哪些材料等的范围定义。但是，当“功”一词出现在物理学语境中时，可以将其视为“做功”。

什么是功？

功和做功主要用于相同的含义。然而，在物理学中，我们使用“做功”，因为它等于力和距离的乘积。必须做功才能获得所覆盖的距离。对吧？当我们只说“功”时，它是对需要做什么、需要哪些材料等的范围定义。但是，当“功”一词出现在物理学语境中时，可以将其视为“做功”。

什么是做功？

当对一个物体施加一个力 F 时，它会沿直线或与直线路径成一定角度移动。如果物体以 $\mathrm{\vartheta}$ 角移动距离 d，则所做的功 W 由以下公式给出

$\mathrm{W=Fd\:Cos(\vartheta)}$

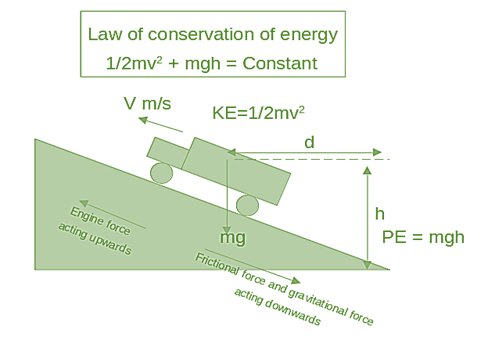
图 1：物体做的功

正如你在上图中看到的，发动机正在对轮胎做功以克服摩擦力。同时，轮胎克服道路摩擦力和重力做功。我们知道摩擦力与卡车的运动方向相反。卡车上没有作用外部力。因此，发动机对轮胎做的有效功抵消了摩擦力和重力，并使卡车以恒定速度 V 向前移动。由于卡车以稳定的速度行驶，因此动能没有变化 $\mathrm{(\Delta\:V=0)}$。因此，根据功能定理，没有做功。可以注意到，随着卡车爬坡，势能头 (mgh) 正在增加，从而保持了守恒定律。

做功的类型

定义了三种类型的功。它们是正功、负功和零功。当物体的位移方向与所施加力的方向相同，则为正功。当物体的位移方向与所施加外力的方向相反时，则为负功。当即使对物体施加外力，位移也为零时，则为零功。

示例

什么时候我们说功是负功？

举个例子，当你试图将一辆手推车推上坡时，假设由于手推车中货物的重量，你正在向下滑动。尽管你向上推着它，但手推车仍在缓慢地向下滚动。这是一种负功的情形。

正功的例子是什么？一个人爬树是正功，因为位移方向与人向上施加力的方向相同。

最后，让我们看一个零功的例子。据说，当一个人拿着一个袋子静止不动时，所做的功为零。由于重力，袋子的重量向下作用，但由于没有位移，因此所做的功为零。移动物体是正功。

什么是动能？

这是物体在运动过程中获得的能量。与静止物体相关的能量是势能。只要有运动，就有动能。例如，放风筝、飞机飞行、鸟类飞行、赛车、旋转风车、移动的云、行走、游泳、跑步、轨道卫星、瀑布等等。时钟的摆动是动能和势能相互作用的一个例子。当摆锤位于底部中心时，势能为零，动能最大。在两端，动能为零，势能最大 (mgh)。

所有其他能量，如化学能、热能、机械能、电能等，都是势能和动能的组合。在任何时间点，这些能量的总和都是一个常数，这就是能量守恒定律。

功能定理

该定理指出，对物体所做的功等于其动能的变化。所做的功以焦耳为单位测量，在公式中表示为

$\mathrm{W=\Delta K=\frac{1}{2}m(v^2-u^2)=m\times a \times d=F \times d}$

已解决示例

序号	本节中使用的函数	公式
1	动能	$\mathrm{KE=\frac{1}{2}mv^2}$
2	做功	$\mathrm{W=Fd}$

• 一辆重 1500 公斤的卡车以 18 公里/小时的速度行驶，试图用 20000 牛顿的制动力刹车停下。卡车在完全停止前将移动多远？

$\mathrm{初始动能 =\frac{1}{2}\times 1500 \times (18 \times 60 \times 60/1000)^2=18750\:焦耳}$

最终动能 = 0，因为最终速度为零

动能变化 = 18750 - 0 = 18750 焦耳

制动能量（力）所做的功为 20000 牛顿，这等于动能的变化

$\mathrm{F\times\:d=W=18750}$

$\mathrm{20000\times\:d=18750}$

$\mathrm{d=18750/20000=0.9375 \:米}$

• 一个重 50 公斤的物体以 5 米/秒的速度运动。在运动方向上施加 200 牛顿的力，作用距离为 30 米。物体的最终速度是多少？

$\mathrm{所做的功 =F\:\times\:d = 200\:\times\:30 = 6000\:焦耳}$

应用功能定理，

$\mathrm{6000 = 1/2\:\times\:50\:\times\:{v_f}^2 - 1/2 \:\times\:50\:\times\:5^2 }$

$\mathrm{{v_f}^2=265}$

$\mathrm{最终速度,\:v_f=\sqrt{265}=16.27 米/秒}$

结论

本文全面概述了动能和功的概念，特别是由于功能定理将它们联系在一起。对不同类型的功和已解决的示例进行了广泛的讨论。本文阐明了功、做功、功率、能量等相关术语之间的区别，以便获得全面的理解。作为已解决示例部分的序言，列出了所用公式以供参考。常见问题解答和总结提供了其他信息和要点。

常见问题解答

Q1. 能量和功之间有什么关系？

A1. 当物体的动能发生变化时，它必须等效于对物体所做的净功。例如，在直线碰撞中，两个物体彼此靠近并发生碰撞。所做的总功等于冲击力乘以冲击过程中行进的距离。

即平均冲击力 x 行进距离 = 动能变化。

Q2. 如果一个球被踢出并以恒定速度移动 50 米，则踢球者所做的功是多少？

A2. 由于速度恒定，动能的变化变为零。因此，根据功能定理，所做的功也为零。$\mathrm{\Delta W=\Delta K E}$

Q3. 动能有哪些不同的类型？

A3. 光和声、电和热、机械运动。

Q4. 当弹簧从未拉伸状态拉伸到其长度的两倍时，它会储存什么能量？

A4. 当弹簧被拉伸时，阻力（如弹簧张力）会储存势能。

Q5. 力和功的 SI 单位是什么？

A5. 力以牛顿为单位测量。SI 单位为 $\mathrm{kg\:m\:s^{-2}}$。功以焦耳为单位测量。SI 单位为牛顿米或 $\mathrm{kg \:m^2\:s^{-2}}$。