简谐运动和匀速圆周运动

---

引言

简谐运动可以定义为一个质点沿直线作周期性运动，其加速度的方向始终指向该直线上的一固定点，并且加速度的大小与其到该固定点的距离成正比。另一方面，匀速圆周运动指的是一个粒子以恒定的速度沿着圆形路径运动。在这种情况下，粒子的速度大小保持不变，但其速度方向却在不断变化。可以这样说，如果粒子保持圆周运动，那么它的投影将被认为是在做简谐运动。

什么是简谐运动？

简谐运动指的是粒子在平衡位置附近来回重复的运动，其最大位移在平衡位置一侧与另一侧相等。每次振动的周期时间相同（Narinder, Bechinger & Gomez-Solano, 2018）。

根据 Nuryantini 等人（2020）的研究，导致运动的力指向平衡位置，并且该力与粒子偏离平衡位置的距离成正比。其公式为 𝑭 = −𝒌𝒙。其中，F 表示力，x 表示位移，K 表示常数。这种关系被称为胡克定律。

什么是匀速圆周运动？

匀速圆周运动指的是一个粒子沿着圆形路径运动，并且其加速度大小恒定。物体的加速度大小保持不变，不会增加或减小。

匀速圆周运动通常指的是物体沿圆形路径运动。正如 Mutsvangwa（2020）所述，在物体的圆周运动中，速度大小通常保持不变，不存在切向加速度，而向心加速度（径向）加速度为 ω2r。在匀速圆周运动中，由于方向的变化，物体处于加速状态。这些物体正在改变其速度，无论是速度大小还是方向。

简谐运动和匀速圆周运动之间的关系

简谐运动和匀速圆周运动是两种重要的运动，用于描述特定组件的运动。正如 Suleiman（2018）所述，下图可以帮助更好地理解这两种圆周运动。

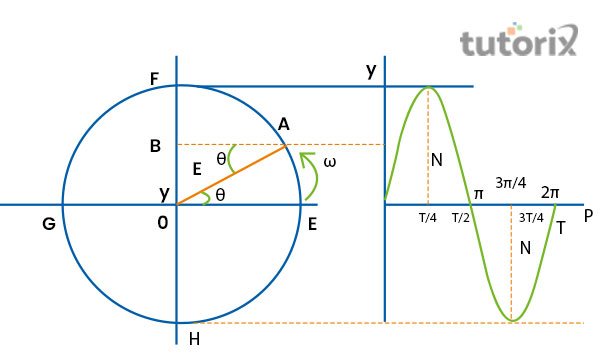
图 1：简谐运动和匀速圆周运动之间的关系

在此，粒子 A 沿圆形路径运动，B 位于直径 FOH 上。直径 FOH 随着直径 FOH 一起振动。

因此，粒子的速度为：

v = dy/dt = d/dt (E sin ωt) = E ω cos ωt

加速度 (a) = dv/dt = d2y/dt2

= – A ω2 sin ωt = – ω2y

这表明粒子的加速度与位移成正比，因此运动 B 表示简谐运动。O 表示平衡位置，F 和 H 表示端点位置。P 表示生成点。圆形称为参考圆，粒子称为参考粒子。需要注意的是，当粒子完成沿着 EFGHE 的一次旋转后，端点 B 完成沿着直径 OFHOHO 的运动，然后返回到其初始位置。

所以，T ∞ 2π/ω [θ = ωt 且当 θ = 2π 时，t = T，所以，2π = ωT]

简谐运动和匀速圆周运动的实际例子

当一个物体在相同的时间内来回运动时，称为简谐运动。正如 Afandi（2018）所述，钟摆的运动持续地来回摆动。简单钟摆的摆动指的是简谐运动。当钟摆被拉开然后从平衡位置释放时，由于重力的影响，它在垂直平面内运动。

围绕太阳旋转的行星的运动是匀速圆周运动的一个突出例子。行星遵循固定的圆形轨道，该轨道充当圆形的边界。太阳位于圆形路径的中心。电子绕原子核的运动、风车叶片的旋转以及巨型轮子的旋转都是匀速圆周运动的一些实际例子。

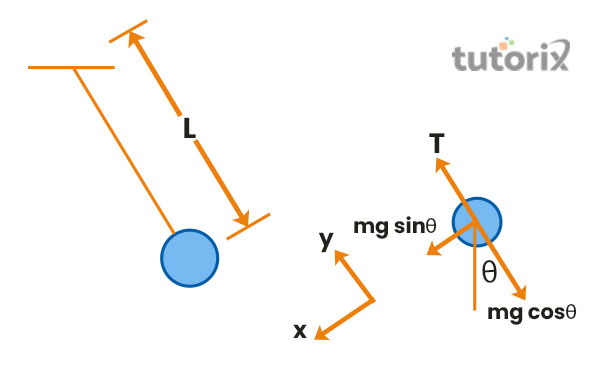
图 2：简谐运动

结论

匀速圆周运动和简谐运动非常重要，因为它们在各种物体的运动中起着重要作用。匀速圆周运动表示物体以恒定速度沿圆形路径运动。

常见问题

Q1. 哪个圆周运动可以用在圆形跑道上跑步来解释？

A1：匀速圆周运动可以通过它来描述。当运动员沿着圆形跑道跑步时，他或她应该表现出圆周运动，因为该运动员的特定运动与跑道的中心点等距。

Q2. 简谐运动的重要性是什么？

A2：这种运动是进行研究以模拟振荡的一个很好的近似值。它在物理学中具有非常重要的意义。许多事物遵循简谐运动的规则，例如吉他等乐器也遵循简谐运动。

Q3. 振荡频率的公式是什么？

A3：f = 1/T = ω/2π 是振荡频率的公式。振荡频率表示粒子每秒执行的振荡次数。

Q4. 简谐运动和匀速圆周运动的意义是什么？

A4：这两种谐波运动对于理解粒子的运动和移动至关重要。这两种运动在物质的加速中起着重要作用。各种运动的运动可以通过实施这两种运动来描述。当物体在平衡位置前后移动时，会发生简谐运动。它在恢复力的作用下，该力与粒子的位移成正比。