数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究什么是推导？
推导是指用产生式规则的右侧替换给定字符串的非终结符。从开始符号生成完整终结符字符串的规则应用序列称为推导。
它可以从开始符号开始推导出终结符字符串，通过重复地用某个产生式替换变量。CFG 的语言是我们能够推导出的终结符集合。这种语言称为上下文无关语言。
推导用 ⇒ 表示。
例如，考虑一个语法。
G=({S},{a,b},P,S)，其中，P 包含以下产生式 -
P={S→aSa |bSb | ∈}
在上面，S 可以被替换为 aSa 或 bSb 或 ∈。
推导类型
推导有两种类型，如下所示 -
- 最左推导
如果我们在每一步都只对最左边的变量使用产生式，则推导 A⇒*w 被称为最左推导。这里，* 表示 0、1、2、……n 个推导。
- 最右推导
如果我们在每一步都只对最右边的变量使用产生式，则推导 A⇒*w 是最右推导。它也称为**规范推导**。
**示例 1** - 令 G 为一个具有产生式的 CFG。
S → AA A → αB B → b B → ε
找到 (1) 最左
- 字符串**abab**的最右推导。
解决方案
- 最左推导 -
S ⇒lm A $\underline{A}$
⇒lm a $\underline{B}$ A
⇒lm a b $\underline{A}$
⇒lm a b a $\underline{B}$
⇒lm a b a b
- 最右推导
S ⇒rm A $\underline{A}$
⇒rm A a $\underline{B}$
⇒rm $\underline{A}$ a b
⇒rm a $\underline{B}$ a b
⇒rm a b a b
**示例 2** - 为回文语言编写上下文无关语法。
L={w c wR| w ∈ {a,b}*} 具有中间符号 c。这里 R 表示字符串的反转。
解决方案
语言表示一个具有中间符号“c”的回文。
∴ **语法 G**=(V,∑,P,S) 将具有产生式。
S → a S a S → b S b S → c
例如，要生成回文 a b c b a，推导为
S ⇒ a $\underline{S}$ a
⇒ a b $\underline{S}$ b a
⇒ a b c b a
**示例 3** - 为生成二进制数字回文的语言编写 CFG。
解决方案
S → 0 S 0 | 1 S 1 S → 0 | 1 | ε
例如，要生成字符串 0 1 1 0，推导为
S ⇒ 0 S 0 ⇒ 0 1 S 1 0 ⇒ 0 1 ε 1 0 ⇒ 0 1 1 0
**示例 4** - 考虑下面给出的语法 -
E → E+E|E * E|id
查找
- 最左
- 字符串的最右推导。
解决方案
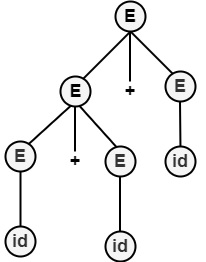
- 最左推导
E ⇒ $\underline{E}$+E
⇒ $\underline{E}$+E+E
⇒ id+E+E
⇒ id+id+E
⇒ id+id+id
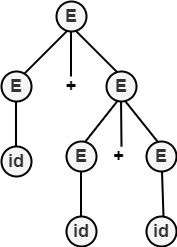
- 最右推导
E ⇒ E+$\underline{E}$
⇒ E+E+$\underline{E}$
⇒ E+E+id
⇒ E+id+id
⇒ id+id+id
3K+ 次查看
