数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
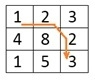
法律研究最小代价路径
给出了一个不同成本的矩阵。此外，还提供了目标单元格。我们必须找到从起始单元格 (0, 0) 到达目标单元格的最小代价路径。
矩阵的每个单元格表示通过该单元格的遍历成本。
从一个单元格出发，我们无法移动到任何地方，我们可以向右移动，也可以向下移动，或者向右下角对角线移动，以到达目的地。
输入和输出
Input: The cost matrix. And the destination point. In this case the destination point is (2, 2). 1 2 3 4 8 2 1 5 3 Output: The minimum cost to reach to the destination from (0, 0). The minimum cost is 8.
算法
minCostPath(destX, destY, cost)
输入 − 目标的 (x, y) 位置和成本矩阵。
输出 − 到达目标的最小成本。
Begin define matrix totalCost, whose order is same as cost matrix totalCost[0, 0] = cost[0, 0] for i := 1 to destX, do totalCost[i, 0] := totalCost[i-1, 0] + cost[i, 0] done for j := 1 to destY, do totalCost[0, j] := totalCost[0, j-1] + cost[0, j] done for all places (i, j) from (1, 1) to (destX, destY), do totalCost[i, j] := minimum of totalCost[i-1, j-1], totalCost[i-1, j] and (totalCost[i, j-1] + cost[i,j]) done return totalCost[destX, destY] End
示例
#include<iostream>
#define ROW 3
#define COL 3
using namespace std;
int cost[ROW][COL] = {
{1, 2, 3},
{4, 8, 2},
{1, 5, 3}
};
int min(int a, int b, int c) {
return (a<b)?((a<c)?a:c):((b<c)?b:c);
}
int minCostPath(int destX, int destY) {
int totalCost[ROW][COL];
totalCost[0][0] = cost[0][0];
for (int i = 1; i <= destX; i++)
totalCost[i][0] = totalCost[i-1][0] + cost[i][0]; //set first col of totalCost array
for (int j = 1; j <= destY; j++) //set first row of totalCost array
totalCost[0][j] = totalCost[0][j-1] + cost[0][j];
for (int i = 1; i <= destX; i++) //for second row and column to all
for (int j = 1; j <= destY; j++)
totalCost[i][j] = min(totalCost[i-1][j-1], totalCost[i- 1][j], totalCost[i][j-1]) + cost[i][j];
return totalCost[destX][destY];
}
int main() {
cout << "Minimum Cost: "<< minCostPath(2, 2); //destination (2, 2)
return 0;
}输出
Minimum Cost: 8
更新时间：17-Jun-2020
553 次浏览
广告