数字电子中的加法器和减法器

---

在数字电子学中，加法器和减法器都是组合逻辑电路（组合逻辑电路是指其输出仅取决于当前输入，而不取决于过去输出的电路），可以进行数字加法或减法运算，更具体地说，是二进制数字的加法或减法。加法器和减法器是处理设备（如微处理器或微控制器）中算术逻辑电路的关键组成部分。在本文中，我们将详细讨论加法器和减法器。

什么是加法器？

我们有不同类型的数字设备，如计算机、计算器，它们可以执行各种处理功能，如加法、减法、乘法、除法等。计算机的算术逻辑单元 (ALU) 执行的最基本算术运算就是两个或多个二进制数的加法。为了执行加法运算，使用了一个名为加法器的组合逻辑电路。

加法器可分为两种类型：

• 半加器
• 全加器

半加器是一种组合逻辑电路，用于执行仅两个比特（二进制数字）的加法。而全加器是一种组合电路，用于执行三个比特（二进制数字）的加法，其中两个是有效位，一个是从先前执行产生的进位。

什么是半加器？

一种设计用于添加两个二进制数字的组合逻辑电路称为半加器。半加器提供输出以及进位值（如果有）。半加器电路是通过连接一个异或门和一个与门来设计的。它有两个输入端和两个输出端，分别用于和与进位。半加器的框图和电路图如图 1 所示。

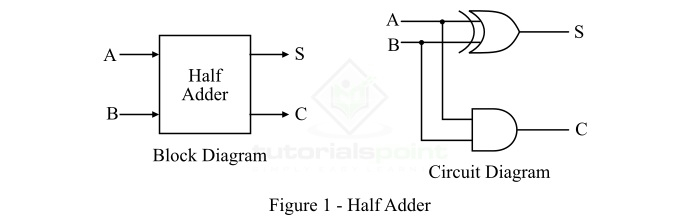
在半加器的情况下，异或门的输出是两个比特的和，与门的输出是进位。尽管一次加法中获得的进位不会转发到下一次加法中，因此它被称为半加器。

半加器的真值表

以下是半加器的真值表：

输入		输出
A	B	S（和）	C（进位）
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

半加器的特性方程

半加器的特性方程，即和 (S) 和进位 (C) 的方程，是根据二进制加法的规则得到的。这些方程如下所示：

半加器的和 (S) 是 A 和 B 的异或。因此，

$$\mathrm{Sum,\, S=A\oplus B=AB'+A'B }$$

半加器的进位 (C) 是 A 和 B 的与。因此，

$$\mathrm{Carry,\, C=A\cdot B }$$

什么是全加器？

可以添加两个二进制数字（比特）和一个进位比特，并产生一个和比特和一个进位比特作为输出的组合逻辑电路称为全加器。

换句话说，一种设计用于添加三个二进制数字并产生两个输出（和与进位）的组合电路称为全加器。因此，全加器电路添加三个二进制数字，其中两个是输入，一个是从前一次加法产生的进位。全加器的框图和电路图如图 2 所示。

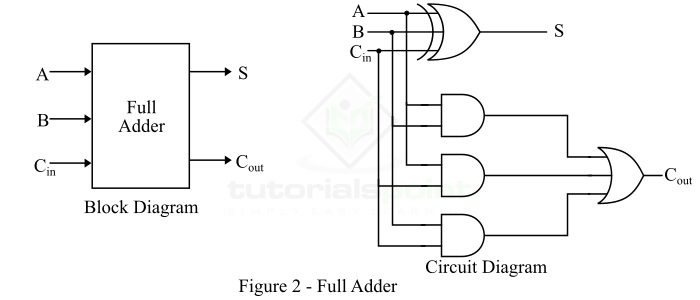
因此，全加器电路由一个异或门、三个与门和一个或门组成，它们按图 2 中的全加器电路所示连接在一起。

全加器的真值表

以下是全加器电路的真值表：

输入			输出
A	B	Cin	S（和）	C（进位）
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

因此，从真值表可以清楚地看出，当且仅当一个输入等于 1 或所有输入都等于 1 时，全加器的和输出才等于 1。而当两个或三个输入等于 1 时，进位输出的进位为 1。

全加器的特性方程

全加器的特性方程，即和 (S) 和进位输出 (C_out) 的方程，是根据二进制加法的规则得到的。这些方程如下所示：

全加器的和 (S) 是 A、B 和 Cin 的异或。因此，

$$\mathrm{Sum,\, S=A\oplus B\oplus C_{in}=A'B'C_{in}+A'BC'_{in}+AB'C'_{in}+ABC_{in} }$$

半加器的进位 (C) 是 A 和 B 的与。因此，

$$\mathrm{Carry,\, C_{out}=AB+AC_{in}+BC_{in}}$$

什么是减法器？

两个二进制数的减法可以通过取输入的 1 的补码或 2 的补码来执行。通过这种方法，减法运算变成了加法运算，因此可以使用加法器电路来执行。这减少了硬件和成本。

在减法运算中，将数字的每个减数位 (B) 从其相应的被减数有效位 (A) 中减去以获得差值位。

与加法器类似，减法器也分为两种类型：

• 半减器
• 全减器

让我们详细讨论一下半减器和全减器。

什么是半减器？

半减器是一种组合逻辑电路，具有两个输入和两个输出（即差和借位）。半减器产生输入处两个二进制位之间的差，并产生借位输出（如果有）。在减法 (A-B) 中，A 称为被减数位，B 称为减数位。半减器的框图和逻辑电路图如图 3 所示。

因此，从逻辑电路图可以清楚地看出，半减器可以使用一个异或门以及一个非门和一个与门来实现。

半减器的真值表

以下是半减器的真值表：

输入		输出
A	B	d（差）	b（借位）
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

半减器的特性方程

半减器的特性方程，即差 (d) 和借位输出 (b) 的方程，是通过遵循二进制减法的规则得到的。这些方程如下所示：

半减器的差 (d) 是 A 和 B 的异或。因此，

$$\mathrm{Difference,\, d=A\oplus B=A'B+AB'}$$

半减器的借位 (b) 是 A'（A 的补码）和 B 的与。因此，

$$\mathrm{Borrow,\, b=A'B}$$

什么是全减器？

全减器是一种组合电路，具有三个输入 A、B、bin 和两个输出 d 和 b。其中，A 是被减数，B 是减数，bin 是前一阶段产生的借位，d 是差输出，b 是借位输出。

由于半减器只能用于查找两个二进制数的最低有效位 (LSB) 的差。因此，如果在 LSB 的减法期间有任何借位，它将影响数字的下一位数的减法。为了克服半减器的这个问题，实现了全减器。全减器的框图和电路图如图 4 所示。

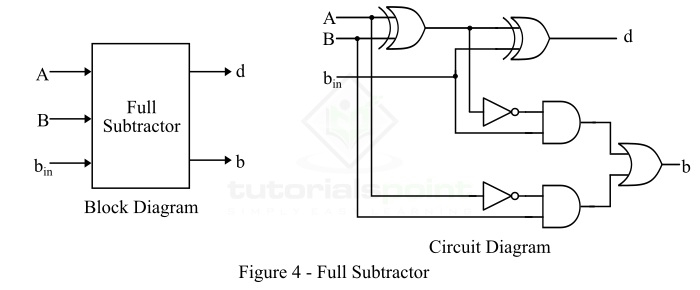
因此，我们可以使用两个异或门、两个非门、两个与门和一个或门来实现全减器。

全减器的真值表

以下是全减器的真值表：

输入			输出
A	B	bin	d（差）	b（借位）
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

全减器的特性方程

全减器的特性方程，即差 (d) 和借位输出 (b) 的方程，是通过遵循二进制减法的规则得到的。这些方程如下所示：

全减器的差 (d) 是 A、B 和 b_in 的异或。因此，

$$\mathrm{Difference,\, d=A\oplus B\oplus b_{in}=A'B'b_{in}+AB'b'_{in}+A'Bb'_{in}+ABb_{in}}$$

全减器的借位 (b) 由下式给出：

$$\mathrm{Borrow,\, b=A'B'b_{in}+A'Bb'_{in}+A'Bb_{in}+ABb_{in}}$$

或

$$\mathrm{Borrow,\, b=A'B\left ( b_{in}+b'_{in} \right )+\left (AB+A'B' \right )b_{in}=A'B+\left (A\oplus B \right )'b_{in}}$$

结论

在本教程中，我们详细讨论了数字电子中的加法器和减法器。我们可以将上述讨论总结为以下几点：

• 一种设计用于添加两个二进制数字的组合逻辑电路称为半加器。

• 能够将两个二进制数字（位）和一个进位位相加，并输出一个和位和一个进位位的组合逻辑电路称为**全加器**。

• **半减器**是一个组合逻辑电路，它有两个输入和两个输出（即差和借位）。

• **全减器**是一个组合电路，它有三个输入A、B、bin和两个输出d和b。

加法器和减法器都是微处理器和微控制器算术逻辑单元中至关重要的逻辑电路。这是因为它们执行两个最基本的算术运算，即二进制数的加法和减法。关于加法器和减法器的另一个重要事项是，它们都是组合逻辑电路，即它们的输出仅取决于当前的输入，而不取决于过去的历史。