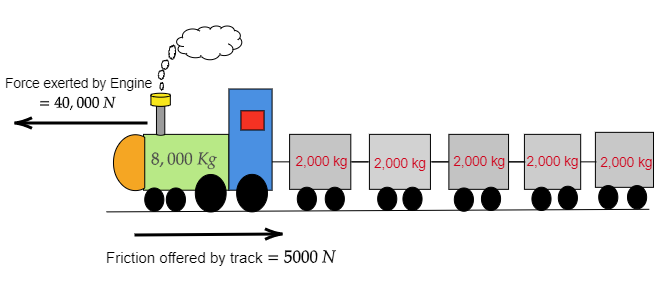
一辆 8000 千克的火车头拉着 5 节车厢，每节车厢重 2000 千克，沿水平轨道行驶。如果火车头施加 40000 牛顿的力，轨道产生 5000 牛顿的摩擦力，那么计算
$(a)$ 净加速力
$(b)$ 火车的加速度。

已知：一辆 8000 千克的火车头拉着 5 节车厢，每节车厢重 2000 千克，沿水平轨道行驶。火车头施加 40000 牛顿的力，轨道产生 5000 牛顿的摩擦力。

要求：计算

$(a)$ 净加速力

$(b)$ 火车的加速度。

解

$(i)$ 已知火车头质量 $m_{engine}=8000\ kg$

每节车厢质量 $m_{wagon}=2000\ kg$

车厢数量 $=5$

火车头施加的力 $F=40000\ N$

轨道产生的摩擦力 $f=5000\ N$

因此，净加速力 $F_{net}=F-f=40,000\ N-5,000\ N=35,000\ N$

$(ii)$ 已知火车头质量 $m_{engine}=8000\ kg$

每节车厢质量 $m_{wagon}=2000\ kg$

车厢数量 $=5$

火车头施加的力 $F=40000\ N$

轨道产生的摩擦力 $f=5000\ N$

因此，净作用力 $F_{net}=F-f=40000\ N-5000\ N=35000\ N$

总质量 $M_{total}=m_{engine}+m_{wagon}$

或 $M_{total}=8000\ kg+5\times2000\ kg$

或 $M_{total}=8000\ kg+10,000\ kg$

或 $M_{total}=18,000\ kg$

因此，加速度 $a=\frac{F_{net}}{M_{total}}$

$=\frac{35,000\ N}{18,000\ kg}$

$=1.94\ m/s^2$

因此，火车的加速度为 $1.94\ m/s^2$。

教程点

更新于： 2022年10月10日

浏览量 114 次

启动你的职业生涯

完成课程获得认证

开始