大欧米茄（Ω）和大西塔（θ）表示法

渐近表示法

渐近表示法用于表示算法的复杂度以进行渐近分析。这些表示法是表示复杂度的数学工具。有三种常用的表示法。

大欧米茄表示法

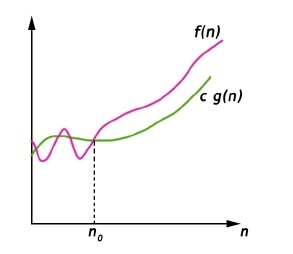
大欧米茄（Ω）表示法给出函数f(n)的常数因数内下界。

我们写f(n) = Ω(g(n))，如果有正常数n₀和c，则n₀右方的f(n)始终位于c*g(n)之上或之上。

Ω(g(n)) = { f(n) : 对于所有n ≤ n₀，存在正常数c和n₀，使得0 ≤ c g(n) ≤ f(n)}

大西塔表示法

大西塔(Θ)表示法给出函数f(n)的常数因数内界限。

我们写f(n) = Θ(g(n))，如果有正常数n₀和c₁和c₂ ，则n₀右方的f(n)始终 nằm giữa c₁*g(n)和c₂*g(n)包括。

Θ(g(n)) = {f(n) : 对于所有n ≥ n₀，存在正常数c₁、c₂和n₀，使得0 ≤ c₁ g(n) ≤ f(n) ≤ c₂ g(n)}

Arnab Chakraborty

更新于： 2019年8月5日

9K+ 浏览

启动你 事业

通过完成课程获得认证

立即开始