数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学C++ 中带括号的二叉树转字符串
在这个问题中，我们给定一个二叉树。我们的任务是创建一个程序，将二叉树转换为 C++ 中带括号的字符串。
二叉树的值是整数，并将以先序遍历的方式提供给程序。字符串应该只包含整数和括号 ()，并且应该是优化的，即所有空括号对都应被消除。
**二叉树**是一种树，其特殊条件是每个节点最多可以有两个子节点。
二叉树示例：
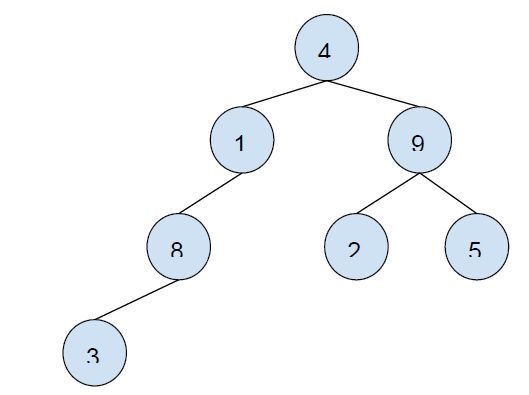
先序遍历：[4, 1, 8, 3, 9, 2, 5]
**让我们举个例子来理解这个问题**
输入
preorder: [4, 1, 8, 3, 9, 2, 5]
输出
解释
Root -> 4()() -> 4(1()())(9) -> 4(1(8()())())(9) -> 4(1(8(3)())())(9) -> 4(1(8(3)())())(9(2)(5))
消除所有空括号：
4(1(8(3)))(9(2)(5))
现在，让我们解决这个问题，我们将进行二叉树的先序遍历，并在必要时放置括号。此外，我们必须消除额外的括号对。为此，我们将使用递归调用一个函数来放置括号。
我们将打印一个节点，并为该节点的两个子节点递归调用该函数，直到该节点没有子节点（即叶子节点）。
在为节点的子节点调用函数时，我们将遇到以下四种情况之一：
**情况 1** - 当节点同时具有左子节点和右子节点时。我们将为两个子节点都放置括号，并将它们的值放在括号内，如果还有子节点，则调用它们的子节点。
示例 - 从上面的例子中，对于根节点 4，其中左右子节点都存在，4(1)(9)。
**情况 2** - 当节点只有左子节点时。我们将左子节点放入括号中，因为没有右子节点，所以它的括号将被消除。并且只调用左子节点的子树（如果有）。
示例 - 从上面的例子中，对于值为 1 的节点，只有左子节点存在，4(1(8()()))(9)。
**情况 3** - 当节点只有右子节点时。我们将为左子节点放置一个空括号。并将右子节点的值放置进去，如果还有子树，则调用它的子树。
**情况 4** - 当节点没有子节点（叶子节点）时。我们不会放置任何括号，只放置值。
**示例** - 从上面的例子中，对于值为 5 的节点，没有子节点，4(1(8(3)))(9(2)(5()()))。
将二叉树转换为带括号的字符串的程序
// 将二叉树转换为带括号的字符串的程序
示例
#include <iostream>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
Node* insertNode(int data){
Node* node = (Node*)malloc(sizeof(Node));
node->data = data;
node->left = node->right = NULL;
return (node);
}
void ConveryBinaryTreeToString(Node* root, string& str){
if (root == NULL)
return;
str.push_back(root->data + '0');
if (!root->left && !root->right)
return;
str.push_back('(');
ConveryBinaryTreeToString(root->left, str);
str.push_back(')');
if (root->right) {
str.push_back('(');
ConveryBinaryTreeToString(root->right, str);
str.push_back(')');
}
}
int main() {
struct Node* root = insertNode(4);
root->left = insertNode(1);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->left->left = insertNode(3);
root->right->left = insertNode(2);
root->right->right = insertNode(5);
string binaryTreeString = "";
ConveryBinaryTreeToString(root, binaryTreeString);
cout<<"The string with preorder traversal of binary tree with brackets is: "<<binaryTreeString;
}输出
The string with preorder traversal of binary tree with brackets is: 4(1(8(3)))(9(2)(5))
400 次浏览
